Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

1:
a: AB<AC
=>góc B>góc C
góc ADB=góc C+góc CAD
góc ADC=góc B+góc BAD
mà góc C<góc B và góc CAD=góc BAD
nên góc ADB<góc ADC
b: Sửa đề; AE=AB
Xét ΔABD và ΔAED có
AB=AE
góc BAD=góc EAD
AD chung
=>ΔABD=ΔAED
=>góc ABD=góc AED

b) Xét ΔABD và ΔAED có
AB=AE(gt)
\(\widehat{BAD}=\widehat{EAD}\)(AD là tia phân giác của \(\widehat{BAE}\))
AD chung
Do đó: ΔABD=ΔAED(c-g-c)
Suy ra: BD=ED(hai cạnh tương ứng)

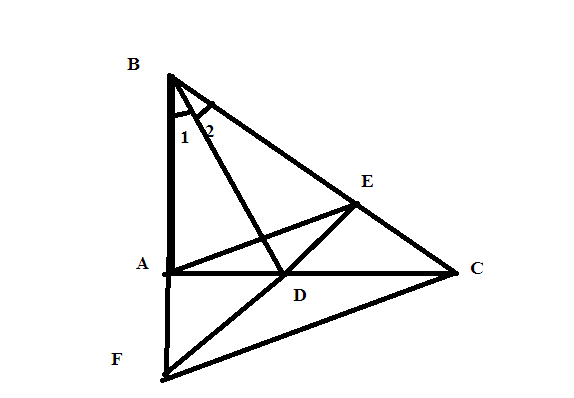
Xét ΔBAD và ΔBDE có:
BD là cạnh chung
B1=B2 (BD là tia phân giác của \(\widehat{B}\))
BA = BE (GT)
Nên ΔBAD= ΔBDE (c.g.c)
=>\(\widehat{ADB}=\widehat{BDE}\)
Ta có:\(\widehat{ADB}+\widehat{ADF}=\widehat{BDF}\)
\(\widehat{BDE}+\widehat{EDC}=\widehat{BDC}\)
Mà :\(\widehat{ADB}=\widehat{BDE}\)(CMT)
\(\widehat{ADF}=\widehat{EDC}\)( 2 góc đối đỉnh)
=>\(\widehat{BDF}=\widehat{BDC}\)
Xét ΔBDF và Δ BDC, có:
\(\widehat{BDF}=\widehat{BDC}\)
BD là cạnh chung
B1=B2
Nên ΔBDF=ΔBDC (g.c.g)
=>DC = DF
b)Ta có:ΔEDC vuông tại E=> DC là cạnh lớn nhất hay DC>DE
MÀ DE=AD (ΔBAD và ΔBDE)
=> AD< DC
c) Ta có BE=BA=>ΔBEA cân tại B
Mà BD là tia phân giác=>BD là đường trung trực
Vì :ΔBDF=ΔBDC=>BF=BC
=>ΔBFC cân tại B=>\(\widehat{C}=\widehat{F}\)
Ta có:\(\widehat{B}+\widehat{C}+\widehat{F}=180^o\)
=>\(\widehat{B}+\widehat{C}.2=180^O\)
=>\(\widehat{C}=\dfrac{180^O-\widehat{B}}{2}\)(1)
vÌ ΔBAE cân tại B
Tương tự ta có:
\(\widehat{E}=\dfrac{180^o-\widehat{B}}{2}\)(2)
Từ (1) và (2)=> \(\widehat{E}=\widehat{C}\)
Mà 2 góc này ở vị trí đồng vị=>AE // FC

a)xet tam giac abd va tam giac aed co
ab=ae
ad la canh chunggoc bad = goc ead
=>tam giác abd = ead
b)gọi i là giao điểm của ad và be
xét tam giác abi và tam giác aei có :
ab=ae
ad là cạnh chung
goc bai = góc eai
=> tam giác abi= tâm giác aei
=>ib=ie =>ad là đường trung trực của be
cho mk 3 đi mk giải tiếp cho, bài nay mk vừa mới kiểm tra
mk giải tiếp nè
theo câu a,b=>góc dbf= góc dec (kề bù do góc abd= aed)
xét tam giác bfd và ecd có
góc dbf= góc dec
bd=ed
bdf=edc
=> tam giác dbf= tam giác ecd
k cho mk đi.mk hứa mk tl hết cho mà
a:AB<AC
=>góc C<góc B
=>góc C+góc CAD<góc B+góc BAD
=>góc ADB<góc ADC
b: Xét ΔABD và ΔAED có
AB=AE
góc BAD=góc EAD
AD chung
=>ΔABD=ΔAED
=>BD=ED
c: Xét ΔABC có AD là phân giác
nên DB/AB=DC/AC
mà AB<AC
nên BD<DC