Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

+) Xét ΔABH và ΔACK, ta có:
AB = AC ( vì tam giác ABC cân tại A)
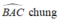
AH = AK (giả thiết)
Suy ra: ΔABH = ΔACK(c.g.c)

+ Do đó, tam giác OBC cân tại O.
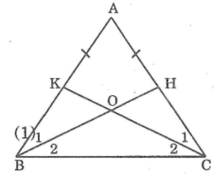

Hình vẽ:
Giải:
Xét \(\Delta ABH\) và \(\Delta ACK\) có:
\(AH=AK\left(gt\right)\)
\(\widehat{A}\) là góc chung
\(AB=AC\) ( Vì \(\Delta ABC\) cân tại \(A\) )
Do đó: \(\Delta ABH=\Delta ACK\left(c.g.c\right)\)
\(\Rightarrow\widehat{B_2}=\widehat{C_2}\) ( cặp góc tương ứng )
Mà \(\widehat{B}=\widehat{C}\) ( Do \(\Delta ABC\) cân tại \(A\) )
\(\Rightarrow\widehat{B}-\widehat{B_2}=\widehat{C}-\widehat{C_2}\)
\(\Rightarrow\widehat{B_1}=\widehat{C_1}\)
\(\Rightarrow\Delta OBC\) cân tại \(O\) . \(\left(đpcm\right)\)

2: góc ABH+góc HBC=góc ABC
góc ACK+góc KCB=góc ACB
mà góc ABC=góc ACB; góc HBC=góc KCB
nên góc ABH=góc ACK

a) Tam giác ABC cân tại A (gt) \(\Rightarrow\widehat{ABC}=\widehat{ACB}\) (Tính chất tam giác cân).
Mà \(\left\{{}\begin{matrix}\widehat{ABC}+\widehat{ABD}=180^o.\\\widehat{ACB}+\widehat{ACE}=180^o.\end{matrix}\right.\)
\(\Rightarrow\widehat{ABD}=\widehat{ACE}.\)
Xét tam giác ABD và tam giác ACE:
+ AB = AC (Tam giác ABC cân tại A).
+ \(\widehat{ABD}=\widehat{ACE}\left(cmt\right).\)
+ BD = CE (gt).
\(\Rightarrow\) Tam giác ABD = Tam giác ACE (c - g - c).
\(\Rightarrow\) AD = AE (Cặp cạnh tương ứng).
\(\Rightarrow\) Tam giác ADE cân tại A (đpcm).
b) Tam giác ADE cân tại A (cmt). \(\Rightarrow\widehat{ADE}=\widehat{AED}\) (Tính chất tam giác cân).
Xét tam giác DHB và tam giác EKC (\(\widehat{DHB}=\widehat{EKC}=90^o\)) :
+ \(\widehat{HDB}=\widehat{KEC}\) (\(\widehat{ADE}=\widehat{AED}\)).
+ BD = CE (gt).
\(\Rightarrow\) Tam giác DHB = Tam giác EKC (cạnh huyền - góc nhọn).
\(\Rightarrow\) BH = CK (Cặp cạnh tương ứng).
Ta có: \(\left\{{}\begin{matrix}AH+HD=AD.\\AK+KE=AE.\end{matrix}\right.\)
Mà HD = KE (Tam giác DHB = Tam giác EKC); AD = AE (cmt).
\(\Rightarrow\) AH = AK \(\Rightarrow\) Tam giác AHK cân tại A. \(\Rightarrow\) \(\widehat{AHK}=\left(180^o-\widehat{A}\right):2.\)
Mà \(\widehat{ADE}=\left(180^o-\widehat{A}\right):2\) (Tam giác ADE cân tại A).
\(\Rightarrow\) \(\widehat{AHK}=\widehat{ADE}.\)
Mà 2 góc này ở vị trí đồng vị.
\(\Rightarrow\) HK // BC (dhnb).
c) Tam giác DHB = Tam giác EKC (cmt). \(\Rightarrow\) \(\widehat{HBD}=\widehat{KCE}\) (2 góc tương ứng).
Mà \(\widehat{HBD}=\widehat{CBO}\); \(\widehat{KCE}=\widehat{BCO}\) (đối đỉnh).
\(\Rightarrow\) \(\widehat{BCO}=\widehat{CBO}\). \(\Rightarrow\) Tam giác OBC là tam giác cân tại O.
d) Xét tam giác ABC cân tại A có: AM là trung tuyến (M là trung điểm BC).
\(\Rightarrow\) AM là đường cao (Tính chất các đường trong tam giác cân).
\(\Rightarrow\) \(AM\perp BC.\) (1)
Xét tam giác OBC cân tại O: OM là trung tuyến (M là trung điểm BC).
\(\Rightarrow\) OM là đường cao (Tính chất các đường trong tam giác cân).
\(\Rightarrow\) \(OM\perp BC.\) (2)
Từ (1) và (2) \(\Rightarrow\) 3 điểm O; A; M thẳng hàng.
\(\Rightarrow\) \(M\in AO.\)
Mà O là giao điểm của BH; CK (gt).
\(\Rightarrow\) O là giao điểm của AM; BH; CK.
\(\Rightarrow\) AM; BH; CK đồng quy (đpcm).

a: Xét ΔAHB vuông tại H và ΔAKC vuông tại K có
AB=AC
góc BAH chung
=>ΔAHB=ΔAKC
=>BH=CK
b: Xét ΔAKO vuông tại K và ΔAHO vuông tại H có
AO chung
AK=AH
=>ΔAKO=ΔAHO
=>góc KAO=góc HAO
=>AO là phân giác của góc KAH

Ta có : AK = AH ; AB = AC ; góc BAC chung
=> Tam giác ABH = tam giác ACK (c.g.c)
=> góc ABH = góc ACK mà góc ABC = góc ACB
=> Góc HBC = góc KCB => góc OBC = góc OCB => Tam giác OBC cân tại O
Bài làm
Xét ΔAHB và ΔAKC có:
AB=AC(gt)
góc A chung
AH=AK(gt)
=>ΔAHB=ΔAKC(c.g.c)
=>ˆABH=ˆACK
Có: ˆB=ˆABH+ˆCBH
ˆC=ˆACK+ˆBCK
Mà ˆB=ˆC(gt)
ˆABH=ˆACK(cmt)
=> ˆCBH=ˆBCK
=>ΔOBC cân tại O