Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a, xét \(\Delta\)BMC và \(\Delta\)AMD có:
\(\widehat{DAM}\)=\(\widehat{MCB}\)(vì so le)
AM=MC(gt)
\(\widehat{AMD}\)=\(\widehat{CMB}\)(vì đối đỉnh)
\(\Rightarrow\)\(\Delta\)BMC=\(\Delta\)AMD(g.c.g)
b,xét tam giác AMB và tam giác CMD có:
AM=MC(gt)
\(\widehat{AMB}\)=\(\widehat{CMD}\)(Vì đối đỉnh)
MB=MD(t.giác BMC=t.giác AMD
=> t.giác AMB=t.giác CMD(c.g.c)
=>AB=CD
vì AB=AC(gt) màAB=CD=> AC=CD
=> t.giác ACD cân tại C

Bài 1: Ta có hình vẽ sau:
a)Xét ΔABM và ΔECM có:
BM = CM (gt)
\(\widehat{AMB}=\widehat{EMC}\) (đỗi đỉnh)
MA = ME (gt)
=> ΔABM = ΔACM (c.g.c) (đpcm)
b) Vì ΔABM = ΔECM (ý a)
=> \(\widehat{MAB}=\widehat{MEC}\) (2 góc tương ứng)
mà 2 góc này lại ở vị trí so le trong nên
=> AB // CE (đpcm)
Bài 5: Ta có hình vẽ sau:
a) Vì OA = OB (gt) và AC = BD (gt)
=> OC = OD
Xét ΔOAD và ΔOBC có:
OA = OB (gt)
\(\widehat{O}\) : Chung
OC = OD (cm trên)
=> ΔOAD = ΔOBC (c.g.c)
=> AD = BC (2 cạnh tương ứng)(đpcm)
b) Vì ΔOAD = ΔOBC(ý a)
=> \(\widehat{OBC}=\widehat{OAD}\) và \(\widehat{ODA}=\widehat{OCB}\)
(những cặp góc tương ứng)
Xét ΔEAC và ΔEBD có:
\(\widehat{OBC}=\widehat{OAD}\) (cm trên)
AC = BD (gt)
\(\widehat{ODA}=\widehat{OCB}\) (cm trên)
=> ΔEAC = ΔEBD (g.c.g) (đpcm)
c) Vì ΔEAC = ΔEBD (ý b)
=> EA = EB (2 cạnh tương ứng)
Xét ΔOAE và ΔOBE có:
OA = OB (gt)
\(\widehat{OBC}=\widehat{OAD}\) (đã cm)
EA = EB (cm trên)
=> ΔOAE = ΔOBE (c.g.c)
=> \(\widehat{AOE}=\widehat{BOE}\) (2 góc tương ứng)
=> OE là phân giác của \(\widehat{xOy}\)

a: Xét ΔMBC và ΔMDA có
góc MAD=góc MCB
MA=MC
góc BMC=góc DMA
=>ΔMBC=ΔMDA
b: Xét tứ giác ABCD có
AD//BC
AD=BC
=>ABCD là hình bình hành
=>AB//CD và AB=CD
=>CA=CD
=>ΔCAD cân tại C
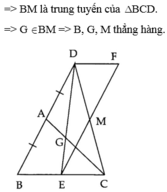
c: Sửa đề: C là trọng tâm
Xét ΔEDB có
EM là trung tuyến
EC=2/3EM
=>C là trọng tâm