Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Để đa thức P(x)=x3+ax2+bx+1 chia hết cho Q(x)=x2+3x+1 thì:
\(\left(b-3a+8\right)x+\left(4-a\right)=0\)
\(\Leftrightarrow\hept{\begin{cases}b-3a+8=0\\4-a=0\end{cases}}\Leftrightarrow\hept{\begin{cases}b-3a=-8\\a=4\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}b-12=-8\\a=4\end{cases}}\Leftrightarrow\hept{\begin{cases}a=4\\b=4\end{cases}}\)
Vậy a = b = 4 thì đa thức P(x)=x3+ax2+bx+1 chia hết cho Q(x)=x2+3x+1

12/
x=2011
=>2012=x+1
thay x+1=2012 ta được:
x2011-(x+1).x2010+(x+1).x2009-(x+1)x2008+...-(x+1).x2+(x+1).x-1
=x2011-x2011-x2010+x2010+x2009-x2009-x2008+...-x3-x2+x2+x-1
=x-1
thay x=2011 ta được:
2011-1=2010
Vậy x2011-2012x2010+2012x2009-2012x2008+...-2012x2+2012x-1=2010

Cau a va b dat cot tim so du .Vi la phep chia het nen du bang 0.Cau c thi da thuc se chia het cho tich (x+3)(x-3) lam tuong tu hai cau a va b

Gỉar sử \(A:B\) được thương là \(4x+c\)
DO \(A⋮B\) nên \(A:B\) được dư bằng 0
Khi đó
\(4x^3+ax^2+bx+5=\left(4x+c\right)\left(x^2-x+1\right)\)
\(=4x^3+cx^2-4x^2-cx+4x+c\)
\(=4x^3+x^2\left(c-4\right)+x\left(4-c\right)+c\)
Áp dụng đồng nhất thức ta có
\(\left\{{}\begin{matrix}a=c-4\\b=4-c\\c=5\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}a=1\\b=-1\end{matrix}\right.\)
Vậy...

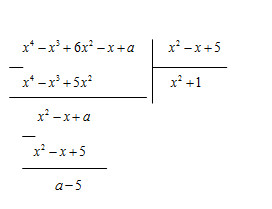
Vậy a = 5 thì đa thức x^4 - x^3 + 6x^2 - x +a chia hết cho đa thức x^2 - x + 5

\(p\left(x\right)=x^4+ax^2+bx+c=\left(x^3-3x^2+3x-1\right)\left(x+3\right)+\left(a+6\right)x^2+\left(b-8\right)x+\left(c+3\right)=\left(x-1\right)^3\left(x+3\right)+\left(a+6\right)x^2+\left(b-8\right)x+\left(c+3\right)\).
Do đó: \(\left(a+6\right)x^2+\left(b-8\right)x+\left(c+3\right)⋮\left(x-1\right)^3\Leftrightarrow a=-6;b=8;c=-3\).