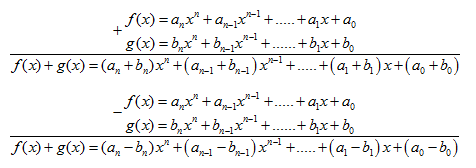Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a. Ta có: f(x) + h(x) = g(x)
Suy ra: h(x) = g(x) – f(x) = (x4 – x3 + x2 + 5) – (x4 – 3x2 + x – 1)
= x4 – x3 + x2 + 5 – x4 + 3x2 – x + 1
= -x3 + 4x2 – x + 6
b. Ta có: f(x) – h(x) = g(x)
Suy ra: h(x) = f(x) – g(x) = (x4 – 3x2 + x – 1) – (x4 – x3 + x2 + 5)
= x4 – 3x2 + x – 1 – x4 + x3 – x2 – 5
= x3 – 4x2 + x – 6

a,f(x)+g(x)=\(\left(a_nx^n+a_{n-1}x^{n-1}+...+a_1x+a_0\right)+\left(b_nx^{n-1}+...+b_1x+b_0\right)\)
=\(a_nx^n+a_{n-1}x^{n-1}+...+a_1x+a_0+b_nx^n+b_{n-1}x^{n-1+...+b_1x+b_0}\)
\(=\left(a_nx^n+b_nx^n\right)+\left(a_{n-1}x^{n-1}+b_{n-1}x^{n-1}\right)+...+\left(a_1x+b_1x\right)+\left(a_0+b_0\right)\)
b
f(x)+g(x)=\(\left(a_nx^n+a_{n-1}x^{n-1}+...+a_1x+a_0\right)+\left(b_nx^n+b_{n-1}x^{n-1}+...+b_1x+b_0\right)\)
\(=a_nx^n+a_{n-1}x^{n-1}+...+a_1x+a_0-b_nx^n-b_{n-1}-b_1x+b_0\)
\(=(a_nx^n-b_nx^n)+(a_{n-1}x^{n-1}-b_{n-1}x^{n-1})+...+(a_1x-b_1x)+\left(a_0+b_0\right)\)
\(=\left(a_n-b_n\right)x^n+(a_{n-1}-b_{n-1})x^{n-1}+...+\left(a_1-b_1\right)x+\left(a_0-b_0\right)\)

a, f(1) = 100 + 99 + ... + 2 + 1 + 1
=> f(x) = (100 + 1) . 100 : 2 + 1 "100 là số số hạng từ 1 -> 100"
=> f(x) = 4951
Hihi..
b, g(1) = 1 + 1 + 1 +...+ 1 + 1 (2016 số 1 theo cách lấy số mũ lớn nhất của x cộng thêm 1)
g(1) = 1 . 2016
g(1) = 2016
g(-1) = 1 + (-1) + (-1)2 + ... + (-1)2014 + (-1)2015
g(-1) = [ 1 + (-1)2 + ... + (-1)2014 ] + [ (-1) + (-1)3 + ... + (-1)2015 ]
g(-1) = [ 1 . 1008 ] + [ (-1) . 1008 ]
g(-1) = 1008 - 1008
g(-1) = 0
k nha!!

\(f\left(x\right)=4x\) ; \(g\left(x\right)=x^2\) \(\Rightarrow f\left(n\right)=4n\) ; \(g\left(n\right)=n^2\)
\(f\left(1\right)+f\left(2\right)+...+f\left(n\right)=4\left(1+2+...+n\right)=\frac{4n\left(n+1\right)}{2}\)
\(=\frac{4n^2+4n}{2}=\frac{4g\left(n\right)+f\left(n\right)}{2}\)

1. a)
\(h\left(0\right)=1+0+0+....+0=1\)
\(h\left(1\right)=1+\left(1+1+....+1\right)\)
( x thừa số 1)
\(=x+1\)
Với x là số chẵn
\(h\left(-1\right)=1+\left(-1\right)+\left(-1\right)^2+\left(-1\right)^3+...+\left(-1\right)^{x-1}+\left(-1\right)^x=1-1+1-1+...-1+1-1=-1\)
Với x là số lẻ
\(h\left(-1\right)=1-1+1-1+1-....+1-1\) =0
b) Tương tự

Bài 3 :
1. Thay x = -5 vào f(x) ta được :
\(\left(-5\right)^2-4\left(-5\right)+5=50\)
Vậy x = -5 không là nghiệm của đa thức trên .
Bài 2 :
1. Ta có : \(f_{\left(x\right)}=x\left(1-x\right)+\left(2x^2-x+4\right)\)
=> \(f_{\left(x\right)}=x-x^2+2x^2-x+4\)
=> \(f_{\left(x\right)}=x^2+4\)
=> \(x^2+4=0\)
Vậy đa thức trên vô nghiệm .
2. Ta có \(g_{\left(x\right)}=x\left(x-5\right)-x\left(x+2\right)+7x\)
=> \(g_{\left(x\right)}=x^2-5x-x^2-2x+7x\)
=> \(g_{\left(x\right)}=0\)
Vậy đa thức trên vô số nghiệm .
3. Ta có : \(h_{\left(x\right)}=x\left(x-1\right)+1\)
=> \(h_{\left(x\right)}=x^2-x+1\)
=> \(h_{\left(x\right)}=\left(x-\frac{1}{2}\right)^2+\frac{3}{4}\)
=> \(\left(x-\frac{1}{2}\right)^2=-\frac{3}{4}\)
Vậy đa thức vô nghiệm .
Bài 3:
\(f\left(x\right)=x^2+4x-5.\)
+ Thay \(x=-5\) vào đa thức \(f\left(x\right)\) ta được:
\(f\left(x\right)=\left(-5\right)^2+4.\left(-5\right)-5\)
\(\Rightarrow f\left(x\right)=25+\left(-20\right)-5\)
\(\Rightarrow f\left(x\right)=25-20-5\)
\(\Rightarrow f\left(x\right)=5-5\)
\(\Rightarrow f\left(x\right)=0.\)
Vậy \(x=-5\) là nghiệm của đa thức \(f\left(x\right).\)
Chúc bạn học tốt!