Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

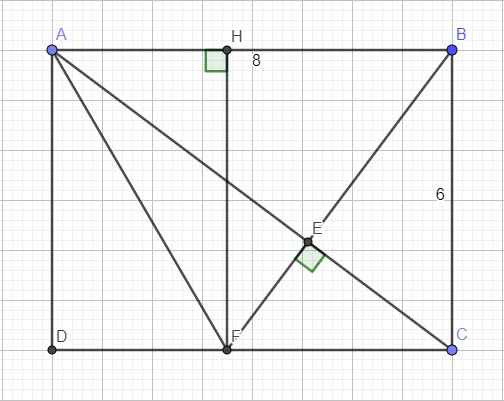
Áp dụng định lý Pitago cho tam giác vuông ABC
\(AC=\sqrt{AB^2+BC^2}=10\left(cm\right)\)
Áp dụng hệ thức lượng cho tam giác vuông ABC với đường cao BE:
\(AB^2=AE.AC\Rightarrow AE=\dfrac{AB^2}{AC}=6,4\left(cm\right)\)
\(AB.AC=BE.AC\Rightarrow AE=\dfrac{AB.AC}{BC}=4,8\left(cm\right)\)
b.
Ta có: \(EC=AC-AE=3,6\left(cm\right)\)
Do AB song song CF, theo định lý Talet:
\(\dfrac{CF}{AB}=\dfrac{CE}{AE}\Rightarrow CF=\dfrac{AB.CE}{AE}=4,5\left(cm\right)\)
\(\Rightarrow DF=DC-CF=8-4,5=3,5\left(cm\right)\)
Áp dụng định lý Pitago cho tam giác vuông ADF:
\(AF=\sqrt{AD^2+DF^2}=\dfrac{\sqrt{193}}{2}\left(cm\right)\)
Pitago tam giác vuông BCF:
\(BF=\sqrt{BC^2+CF^2}=7,5\left(cm\right)\)
Kẻ FH vuông góc AB \(\Rightarrow ADFH\) là hình chữ nhật (tứ giác 3 góc vuông)
\(\Rightarrow FH=AD=6\left(cm\right)\)
\(S_{ABF}=\dfrac{1}{2}FH.AB=\dfrac{1}{2}.6.8=24\left(cm^2\right)\)

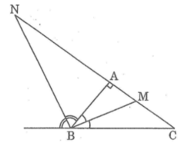
Vì BM là đường phân giác của góc B nên ta có:
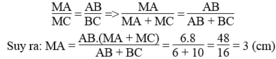
Vì BN là đường phân giác của góc ngoài đỉnh B nên ta có: BM ⊥ BN
Suy ra tam giác BMN vuông tại B
Theo hệ thức liên hệ giữa đường cao và hình chiếu hai cạnh góc vuông, ta có: A B 2 = AM.AN
Suy ra: AN = ![]() = 12 (cm)
= 12 (cm)


Áp dụng định lý Pitago cho ABH vuông tại A có:
![]()
![]()
Vì BM là tia phân giác trong của góc B ⇒ M A M C = A B B C (Tính chất đường phân giác)
⇒ M A M C + M A = A B B C + A B ⇒ M A A C = A B B C + A B ⇒ M A 8 = 6 10 + 6 ⇒ MA = 3cm
Vì BM; BN là tia phân giác trong và ngoài của góc B ⇒ N B M ^ = 90 0
Áp dụng hệ thức lượng trong ABM vuông tại B có đường cao BA ta có:
![]()
Đáp án cần chọn là: D

Vì BM là đường phân giác của góc B nên ta có :
\(\frac{MA}{MC}=\frac{AB}{BC}\Rightarrow\frac{MA}{MA+MC}=\frac{AB}{AB+AC}\)
\(\Rightarrow MA=\frac{AB.\left(MA+MC\right)}{AB+BC}=\frac{6.8}{6+10}=\frac{48}{16}=3\left(cm\right)\)
Vì BN là đường phân giác của góc ngoài đỉnh B nên ta có: \(BM\perp BN\)
Suy ra tam giác BMN vuông tại B
Theo hệ thức liên hệ giữa đường cao và hình chiếu hai cạnh góc vuông, ta có: AB2 = AM . AN
Suy ra: \(AN=\frac{AB^2}{AM}=\frac{6^2}{3}=\frac{36}{3}=12\left(cm\right)\)
Tính được mỗi AM , AN nên thông cảm 😅