Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Áp dụng định luật khúc xạ
\(\sin i =n_t. \sin r_t\)=>\(\sin r_t = \frac{0,8}{n_t}=> r_t \approx 36,56^0\)
\(\sin i =n_d. \sin r_d\) => \(\sin r_d = \frac{0,8}{n_d}=> r_d \approx 36,95^0\)
Bề rộng quang phổ tạo ra dưới đáy bể là
\(TD = HD-HT = OH.(\tan r_d-\tan r_t) \approx 1,257 mm. \)

Đáp án C
Bước sóng của sóng λ = 2 π v ω = 4cm.
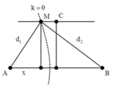
+ Gọi I là một điểm trên MN, phương trình dao động của I có dạng:
u 1 = a 1 cos ω t - π d 1 + d 2 λ .
+ Để I cùng pha với nguồn thì π d 1 + d 2 λ = 2 k π → d 1 + d 2 = 2 k λ = 8k.
Với khoảng giá trị của tổng d 1 + d 2 là O N ≤ d 1 + d 2 ≤ O M + M N .
→ 50 8 ≤ k ≤ 36 + 36 2 + 50 2 8 ↔ 6 , 25 ≤ k ≤ 12 , 2
→ Có 6 điểm dao động cùng pha với nguồn trên MN.

- Ta có:
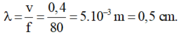
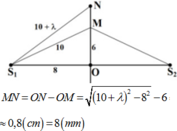
+ Độ lệch pha dao động của 2 điểm M, N trên đường trung trực d của AB là:
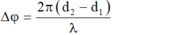
+ N dao động cùng pha với M khi :
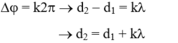
+ Hai điểm M1 và M2 gần M nhất dao động cùng pha với M ứng với:
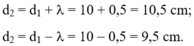
- Ta có:

- Vậy điểm dao động cùng pha gần M nhất ứng với điểm M2 và cách M 8 mm gần 7,8 mm nhất.

+ Ta có: λ = v f = 0 , 4 80 = 5 . 10 - 3 m = 0,5 cm.
+ Độ lệch pha dao động của 2 điểm M, N trên đường trung trực d của AB là: ∆ φ = 2 π ( d 2 - d 1 ) λ
+ N dao động cùng pha với M khi Dj = k2p → d2 - d1 = k λ → d2 = d1 + k λ
+ Hai điểm M1 và M2 gần M nhất dao động cùng pha với M ứng với: d2 = d1 + λ = 10 + 0,5 = 10,5 cm
Và d2 = d1 - λ = 10 - 0,5 = 9,5 cm.
+ Ta có: MM1 = MH - M1H mà M H = 10 2 - 8 2 = 6 cm và M 1 H = 9 , 5 2 - 8 2 = 5 , 12 cm → MM1 = 0,88 cm = 8,8 mm
MM2 = M2H - MH mà M 2 H = 10 , 5 2 - 8 2 = 6 , 8 cm → MM2 = 0,8 cm = 8 mm.
Vậy điểm dao động cùng pha gần M nhất ứng với điểm M2 và cách M 8 mm → gần 7,8 mm nhất.
Đáp án A

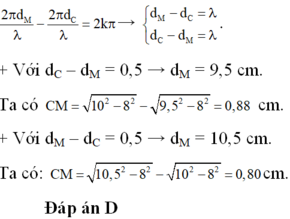


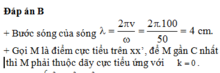
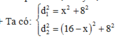
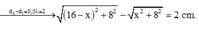
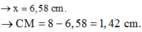
Đáp án C
Ta có hình vẽ
Từ hình vẽ ta thấy rằng IJ = JS’.tani; IJ = JS.tanr
Do