Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án: B
2 x x 2 + 1 ≥ 1 ⇔ 2 x - x 2 - 1 x 2 + 1 ≥ 0 ⇔ 2 x - x 2 - 1 ≥ 0 ⇔ - ( x - 1 ) 2 ≥ 0 ⇔ x = 1 ⇒ A = { 1 } .
∆ ' = b 2 - 4 . Để phương trình vô nghiệm thì
∆ ' < 0 ⇔ b 2 - 4 < 0 ⇔ b 2 < 4 ⇔ - 2 < b < 2 ⇒ B = { - 1 ; 0 ; 1 } . ⇒ A ⊂ B .

(x^2-10x+21)(x^3-x)=0
=>(x-3)(x-7)*x*(x^2-1)=0
=>x thuộc {0;1;-1;3;7}
=>B={0;1;-1;3;7}
Ta có:
\(\left(x^2-10x+21\right)\left(x^2-x\right)=0\)
\(\Leftrightarrow\left(x^2-3x-7x+21\right)x\left(x-1\right)=0\)
\(\Leftrightarrow\left(x-3\right)\left(x-7\right)x\left(x-1\right)=0\) (ĐK: \(x\in Z\))
\(\Leftrightarrow\left[{}\begin{matrix}x=0\left(tm\right)\\x=3\left(tm\right)\\x=7\left(tm\right)\\x=1\left(tm\right)\end{matrix}\right.\)
\(\Rightarrow B=\left\{1;3;7;0\right\}\)

( − 4 ; 3 ] ∩ ℤ = { − 3 ; − 2 ; − 1 ; 0 ; 1 ; 2 ; 3 }
Đáp án A

Ta có :
P(-4) = 2.(-4)2 – 1 = 31 không chia hết cho 7.
P(-3) = 2.( -3)2 -1 = 17 không chia hết cho 7.
P(5) = 2. 52 – 1 = 49 chia hết cho 7.
P(6) = 2.62 – 1 = 71 không chia hết cho 7.
Vậy mệnh đề đúng là P(5).
Đáp án C

a) \(2^n>2n+1\) (1)
Với n=3 thì (1) <=> \(2^3>2.3+1\) (đúng)
Giả sử (1) đúng đến n=k => \(2^k-2k-1>0\)
Ta có: \(2^{k+1}-2\left(k+1\right)-1=2\left(2^k-2k-1\right)+2k-1>0\) (với \(k>3\))
=> \(2^{k+1}>2\left(k+1\right)+1\) (1) đúng đến n=k+1
Theo quy nạp thì (1) đúng
b) \(2^n\ge n^2\) (2)
Với n=4 thì (2) <=> \(2^4\ge4^2\) (đúng)
Giả sử (2) đúng đến n=k => \(2^k-k^2\ge0\)
Ta có: \(2^{k+1}-\left(k+1\right)^2=2\left(2^k-k^2\right)+\left(k-1\right)^2\ge0\)
=> \(2^{k+1}\ge\left(k+1\right)^2\) => (2) đúng đến n=k+1
Theo nguyên lí quy nạp thì (2) đúng



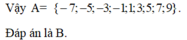
Đáp án A