Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) \(23,3\) phút; \(540^0;27,6^0C\)
b) Khi lấy số trung bình làm đại diện cho các số liệu thống kê về quy mô và độ lớn, có thể xem rằng mỗi ngày bạn A đi từ nhà đến trường đều mất 23,3 phút.
Tương tự, nêu ý nghĩa số trung bình của các số liệu thống kê cho ở bảng 7 và bảng 8.

Nhiệt độ trung bình của tháng 5 ở địa phương A từ 1961 đến hết 1990
| Lớp nhiệt độ (
C
0
) |
Tần số | Tần suất (%) |
| [25; 26) | 1 | 3,3 |
| [26; 27) | 5 | 16,7 |
| [27; 28) | 13 | 43,3 |
| [28; 29) | 9 | 30,0 |
| [29; 30] | 2 | 6,7 |
| Cộng | 30 | 100 (%) |

a) Bảng 6:
| Lớp nhiệt độ (ºC) | Tần suất (%) | Giá trị đại diện |
| [15; 17] | 16,7 | 16 |
| [17; 19) | 43,3 | 18 |
| [19; 21) | 36,7 | 20 |
| [21; 23] | 3,3 | 22 |
| Cộng | 100 (%) |
Số trung bình cộng của bảng 6 là:
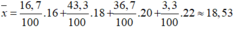
Số trung bình cộng của bảng 8 là:
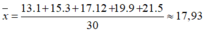
b) Nhiệt độ trung bình của thành phố Vinh trong tháng 12 cao hơn nhiệt độ trung bình trong tháng 2 khoảng 0,6ºC.

a) Nhiệt độ trung bình trong năm ở Hà Nội là: \(\overline X = \frac{{16,4 + 17,0 + 20,2 + 23,7 + 27,3 + 28,8 + 28,9 + 28,2 + 27,2 + 24,6 + 21,4 + 18,2}}{{12}} = 23,5\)
b) Nhiệt độ trung bình của tháng có giá trị thấp nhất là: \(16,4\left( {^oC} \right)\)
Nhiệt độ trung bình của tháng có giá trị cao nhất là: \(28,9\left( {^oC} \right)\)

a) \(\overline{x}=36,5g;s_1-6,73\)
\(M_e=35g;M_0=35g\)
b) Ta chọn số trung bình \(\overline{x}=36,5g\) để làm giá trị đại diện cho các số liệu thống kê đã cho về quy mô và độ lớn
c) Rổ trứng thứ nhất và rổ trứng thứ hai có cùng đơn vị đo và \(\overline{x}_1=\overline{x}_2=36,5g;s_1=6,73g< 10g=s_2\). Suy ra trứng gà ở ổ thứ nhất đồng đều hơn.


c) Trong 60 buổi được khảo sát
Chiếm tỉ lệ thấp nhất (8,33%) là những buổi có dưới 10 người xem
Chiếm tỉ lệ cao nhất (25%) là những buổi có từ 30 người đến dưới 40 người xem
Đa số (78,33%) các buổi có từ 10 người đến dưới 50 người xem
d) \(\overline{x}\approx32\) người; \(s^2\approx219,7;s=15\) người












Đáp án: 36,7%