Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Ta có 3 – 2 < 6 < 3 + 2 bất đẳng thức này sai nên ba độ dài 2cm, 3cm, 6cm không là ba cạnh của tam giác.
b) Vì 6 = 2 + 4 nên ba độ dài là 2cm, 4cm, 6cm không là 3 cạnh của một tam giác
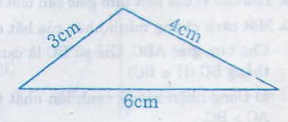
c) 4 – 3 < 6 < 4 + 3 bất đẳng thức đúng nên ba độ dài 3cm, 4cm, 6cm là 3 cạnh của một tam giác.
a) Nhận xét: 2cm + 3cm = 5cm < 6cm nên bộ ba đoạn thẳng dài 2cm, 3cm, 6cm không phải là bộ ba cạnh của một tam giác.
b) Nhận xét: 2cm + 4cm = 6cm = 6cm nên bộ ba đoạn thẳng dài 2cm, 4cm, 6cm không phải là bộ ba cạnh của một tam giác.
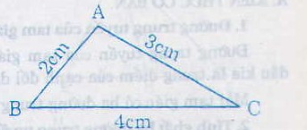
c) Nhận xét: 3cm + 4cm = 7cm > 6cm nên bộ ba đoạn thẳng dài 3cm, 4cm, 6cm là bộ ba cạnh của một tam giác.


a) Với 3 độ dài 2cm, 3cm, 4cm lập thành 3 cạnh của tam giác.
b) 1cm; 2cm; 3,5cm không lập thành 3 cạnh của tam giác vì 2 – 1 < 3,5 < 2 + 1 bất đẳng thức sai
c) 2,2 + 2 = 4,2 không lập thành tam giác

a) Vì 5+4 > 6 nên ba độ dài 5 cm, 4 cm, 6 cm có thể là độ dài ba cạnh của một tam giác.

b) Vì 3 + 6 = 9 < 10 nên ba độ dài 3 cm, 6 cm, 10 cm không thể là độ dài ba cạnh của một tam giác

2: BC=căn 6^2+8^2=10cm
3:
a: 5cm; 12cm; 9cm
5+12>9; 5+9>12; 12+9>5
=>Bộ ba số này thỏa mãn độ dài 3 cạnh của 1 tam giác
b: 12+16>20; 12+20>16; 20+16>12
=>Bộ ba số này thỏa mãn độ dài 3 cạnh của 1 tam giác
4:
Xét ΔABD và ΔACE có
AB=AC
góc BAD chung
AD=AE
=>ΔABD=ΔACE
10:
a: AB=căn 10^2-6^2=8cm
b: Xét ΔMAC và ΔMDB có
MA=MD
góc AMC=góc DMB
MC=MB
=>ΔMAC=ΔMDB
c: Xét tứ giác ABDC có
M là trung điểm chung của AD và BC
=>ABDC là hbh
=>AB//CD

Để tạo được một tam giác thì độ dài ba cạnh phải thoả mãn bất đẳng thức tam giác đó là tổng độ dài hai cạnh bất kỳ phải lớn hơn cạnh còn lại.
Vì vậy chỉ có bộ ba độ dài sau thoả mãn (2,3,4); (2,4,5); (3,4,5).
(Lưu ý: để xét cho nhanh, các bạn áp dụng phần Lưu ý (trang 63 sgk Toán 7 Tập 2)), tức là ta so sánh độ dài lớn nhất với tổng hai cạnh hoặc so sánh độ dài nhỏ nhất với hiệu hai cạnh.
Ví dụ với cặp 3 độ dài (1, 2, 3) không là ba cạnh vì:
- bất đẳng thức 3 > 2 + 1 sai
- hoặc bất đẳng thức 3 - 2 < 1 sai)
Trong một tam giác, độ dài một cạnh lớn hơn hiệu và nhỏ hơn tổng của hai cạnh còn lại. Vậy nên với năm đoạn thẳng có độ dài 1cm, 2cm, 3cm, 4cm, 5cm chỉ dựng được tam giác với ba cạnh là các đoạn thẳng có độ dài là các bộ ba 2cm, 3cm, 4cm, bộ ba 3cm, 4cm, 5cm, bộ ba 2cm, 4cm, 5cm.

Ta có : 4cm + 3cm = 7cm > 6cm.
⇒ Bộ ba đoạn thẳng 3cm, 4cm, 6cm thỏa mãn bất đẳng thức tam giác nên là ba cạnh của tam giác.
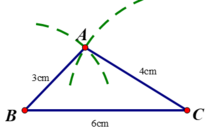
Cách dựng tam giác có ba độ dài 3cm, 4cm, 6cm
- Vẽ BC = 6cm
- Dựng đường tròn tâm B bán kính 3cm ; đường tròn tâm C bán kính 4cm. Hai đường tròn cắt nhau tại A. Nối AB, AC ta được tam giác cần dựng.

Vì 6cm = 2cm + 4cm
⇒ Bộ ba đoạn thẳng 2cm, 4cm, 6cm không thỏa mãn bất đẳng thức tam giác nên không phải là ba cạnh của tam giác.

Ta có: 3cm + 2cm = 5cm < 6cm
⇒ Bộ ba đoạn thẳng 2cm, 3cm, 6cm không thỏa mãn bất đẳng thức tam giác nên không phải là ba cạnh của tam giác.
Theo bất đẳng thức tam giác:
a) Vì 2 + 3 = 5 nên bộ ba đoạn thẳng có độ dài 2 cm, 3 cm, 5 cm không thể là độ dài ba cạnh của một tam giác
b) Vì 3+4 > 6 nên bộ ba đoạn thẳng có độ dài 3 cm, 4 cm, 6 cm có thể là độ dài ba cạnh của một tam giác
* Cách vẽ: + Vẽ độ dài cạnh AB = 6cm.
+ Dùng compa, vẽ cung tròn tâm A bán kính 3 cm, cung tròn tâm B bán kính 4cm. Hai cung tròn này cắt nhau tại C.
Ta được tam giác ABC cần vẽ.
c) Vì 2+4 > 5 nên bộ ba đoạn thẳng có độ dài 2 cm, 4 cm, 5 cm có thể là độ dài ba cạnh của một tam giác
* Cách vẽ: + Vẽ độ dài cạnh AB = 5cm.
+ Dùng compa, vẽ cung tròn tâm A bán kính 2 cm, cung tròn tâm B bán kính 4cm. Hai cung tròn này cắt nhau tại C.
Ta được tam giác ABC cần vẽ.