Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(a,P\) xác định \(\Leftrightarrow\left[{}\begin{matrix}x>0\\x\ne1\\x\ne4\end{matrix}\right.\)
\(b,P=\left(\dfrac{1}{\sqrt{x}-1}-\dfrac{1}{\sqrt{x}}\right):\left(\dfrac{\sqrt{x}+1}{\sqrt{x}-2}-\dfrac{\sqrt{x}+2}{\sqrt{x}-1}\right)\\ =\dfrac{\sqrt{x}-\sqrt{x}+1}{\sqrt{x}\left(\sqrt{x}-1\right)}:\dfrac{\left(\sqrt{x}+1\right)\left(\sqrt{x}-1\right)-\left(\sqrt{x}+2\right)\left(\sqrt{x}-2\right)}{\left(\sqrt{x}-2\right)\left(\sqrt{x}-1\right)}\\ =\dfrac{1}{\sqrt{x}\left(\sqrt{x}-1\right)}.\dfrac{\left(\sqrt{x}-2\right)\left(\sqrt{x}-1\right)}{x-1-x+4}\\ =\dfrac{1}{\sqrt{x}}.\dfrac{\sqrt{x}-2}{3}\\ =\dfrac{\sqrt{x}-2}{3\sqrt{x}}\)
\(c,P=\dfrac{1}{4}\Leftrightarrow\dfrac{\sqrt{x}-2}{3\sqrt{x}}=\dfrac{1}{4}\\ \Leftrightarrow\dfrac{4\left(\sqrt{x}-2\right)-3\sqrt{x}}{12\sqrt{x}}=0\\ \Leftrightarrow4\sqrt{x}-8-3\sqrt{x}=0\\ \Leftrightarrow\sqrt{x}=8\\ \Leftrightarrow x=64\left(tmdk\right)\)
Vậy \(x=64\) thì \(P=\dfrac{1}{4}\)

a) ĐKXĐ: \(\left\{{}\begin{matrix}x>0\\x\ne1\end{matrix}\right.\)
Ta có: \(P=\left(\dfrac{\sqrt{x}}{\sqrt{x}-1}-\dfrac{1}{x-\sqrt{x}}\right)\cdot\left(\dfrac{1}{1+\sqrt{x}}+\dfrac{2}{x-1}\right)\)
\(=\left(\dfrac{x}{\sqrt{x}\left(\sqrt{x}-1\right)}-\dfrac{1}{\sqrt{x}\left(\sqrt{x}-1\right)}\right)\cdot\left(\dfrac{\sqrt{x}-1}{\left(\sqrt{x}+1\right)\left(\sqrt{x}-1\right)}+\dfrac{2}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\right)\)
\(=\dfrac{x-1}{\sqrt{x}\left(\sqrt{x}-1\right)}\cdot\dfrac{\sqrt{x}-1+2}{\left(\sqrt{x}+1\right)\left(\sqrt{x}-1\right)}\)
\(=\dfrac{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}{\sqrt{x}\left(\sqrt{x}-1\right)}\cdot\dfrac{\sqrt{x}+1}{\left(\sqrt{x}+1\right)\left(\sqrt{x}-1\right)}\)
\(=\dfrac{\sqrt{x}+1}{\sqrt{x}\left(\sqrt{x}-1\right)}\)
b) Để P>0 thì \(\dfrac{\sqrt{x}+1}{\sqrt{x}\left(\sqrt{x}-1\right)}>0\)
mà \(\sqrt{x}+1>0\forall x\) thỏa mãn ĐKXĐ
nên \(\sqrt{x}\left(\sqrt{x}-1\right)>0\)
mà \(\sqrt{x}>0\forall x\) thỏa mãn ĐKXĐ
nên \(\sqrt{x}-1>0\)
\(\Leftrightarrow\sqrt{x}>1\)
hay x>1
Kết hợp ĐKXĐ,ta được: x>1
Vậy: Để P>0 thì x>1

Điều kiện: x>2
P= \(\left(\dfrac{1}{\sqrt{x}-1}-\dfrac{1}{\sqrt{x}}\right):\left(\dfrac{\sqrt{x}+1}{\sqrt{x}-2}-\dfrac{\sqrt{2}+2}{\sqrt{x}-1}\right)\)
P= \(\left(\dfrac{\sqrt{x}-\sqrt{x}+1}{\sqrt{x}\left(\sqrt{x}-1\right)}\right):\left(\dfrac{x-1-x+4}{\left(\sqrt{x}-2\right)\left(\sqrt{x}-1\right)}\right)\)
P= \(\dfrac{1}{\sqrt{x}\left(\sqrt{x}-1\right)}.\dfrac{\left(\sqrt{x}-2\right)\left(\sqrt{x}-1\right)}{3}\)
P= \(\dfrac{\sqrt{x}-2}{3\sqrt{x}}\)
b) P= \(\dfrac{1}{4}\)
⇔\(\dfrac{\sqrt{x}-2}{3\sqrt{x}}\) =\(\dfrac{1}{4}\)
⇔\(4\sqrt{x}-8=3\sqrt{x}\)
⇔\(\sqrt{x}=8\)
⇔x=64 (TM)
Vậy X=64(TMĐK) thì P=\(\dfrac{1}{4}\)

a, x > 0 ; x khác 1
\(P=\left(\dfrac{\sqrt{x}}{\sqrt{x}-1}-\dfrac{2}{x-\sqrt{x}}\right):\dfrac{1}{\sqrt{x}-1}\)
\(=\left(\dfrac{x-2}{\sqrt{x}\left(\sqrt{x}-1\right)}\right):\dfrac{1}{\sqrt{x}-1}=\dfrac{x-2}{\sqrt{x}}\)
b, Ta có : \(P=\dfrac{x-2}{\sqrt{x}}=1\Rightarrow x-2=\sqrt{x}\)
\(\Leftrightarrow x-\sqrt{x}-2=0\Leftrightarrow\left(\sqrt{x}+1>0\right)\left(\sqrt{x}-2\right)=0\Leftrightarrow x=4\)(tm)
a: \(P=\dfrac{x-2}{\sqrt{x}\left(\sqrt{x}-1\right)}\cdot\dfrac{\sqrt{x}-1}{1}=\dfrac{x-2}{\sqrt{x}}\)
b: Để P=1 thì \(x-\sqrt{x}-2=0\)
hay x=4

\(P=\left(\dfrac{1}{x-\sqrt{x}}+\dfrac{1}{\sqrt{x}-1}\right):\dfrac{\sqrt{x}}{x-2\sqrt{x}+1}\left(x>0;x\ne1\right)\)
\(a,P=\left(\dfrac{1}{x-\sqrt{x}}+\dfrac{1}{\sqrt{x}-1}\right):\dfrac{\sqrt{x}}{x-2\sqrt{x}+1}\)
\(=\left[\dfrac{1}{\sqrt{x}\left(\sqrt{x}-1\right)}+\dfrac{\sqrt{x}}{\sqrt{x}\left(\sqrt{x}-1\right)}\right]:\dfrac{\sqrt{x}}{\left(\sqrt{x}-1\right)^2}\)
\(=\dfrac{\sqrt{x}+1}{\sqrt{x}\left(\sqrt{x}-1\right)}.\dfrac{\left(\sqrt{x}-1\right)^2}{\sqrt{x}}\)
\(=\dfrac{x-1}{x}\)
\(b,P>\dfrac{1}{2}\Rightarrow\dfrac{x-1}{x}>\dfrac{1}{2}\Leftrightarrow2x-2>x\Leftrightarrow x>2\)

ĐKXĐ: \(x\ge0,x\ne1\)
a) \(P=\left[\dfrac{2\sqrt{x}}{\left(\sqrt{x}-1\right)\left(x+1\right)}-\dfrac{1}{\sqrt{x}-1}\right]:\left(\dfrac{x+1+\sqrt{x}}{x+1}\right)\)
\(=\dfrac{2\sqrt{x}-x-1}{\left(\sqrt{x}-1\right)\left(x+1\right)}.\dfrac{x+1}{x+\sqrt{x}+1}=\dfrac{-\left(\sqrt{x}-1\right)^2}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}=\dfrac{1-\sqrt{x}}{x+\sqrt{x}+1}\)
\(P=\dfrac{1-\sqrt{x}}{x+\sqrt{x}+1}< 0\Leftrightarrow1-\sqrt{x}< 0\Leftrightarrow\sqrt{x}>1\Leftrightarrow x>1\)

a: Ta có: \(P=\left(\dfrac{2\sqrt{x}}{\sqrt{x}+3}+\dfrac{\sqrt{x}}{\sqrt{x}-3}-\dfrac{3x+3}{x-9}\right):\left(\dfrac{2\sqrt{x}-2}{\sqrt{x}-3}-1\right)\)
\(=\dfrac{2x-6\sqrt{x}+x+3\sqrt{x}-3x-3}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}\cdot\dfrac{\sqrt{x}-3}{2\sqrt{x}-2-\sqrt{x}+3}\)
\(=\dfrac{-3\left(\sqrt{x}+1\right)}{\sqrt{x}+3}\cdot\dfrac{1}{\sqrt{x}+1}\)
\(=\dfrac{-3}{\sqrt{x}+3}\)

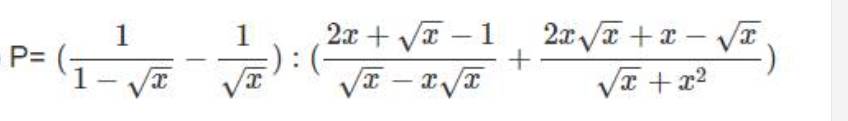
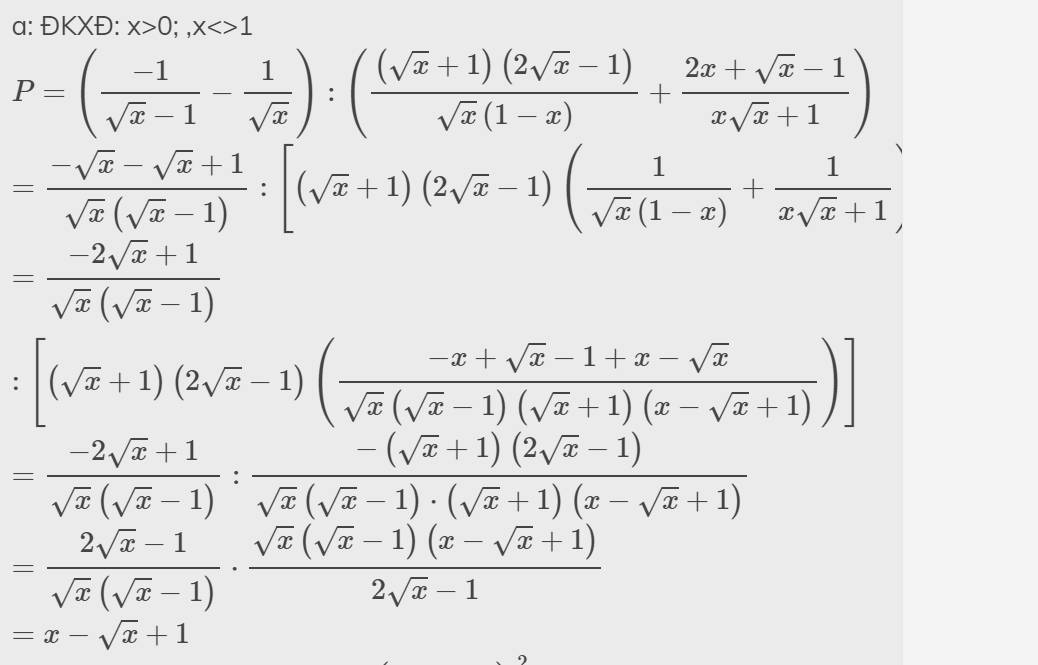
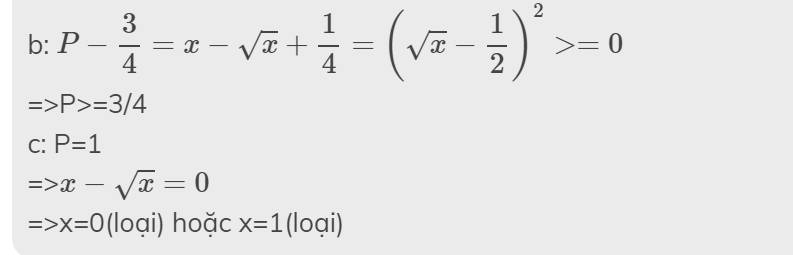
\(a,P=\left(\dfrac{x-2\sqrt{x}+1}{\sqrt{x}-1}+\dfrac{2\sqrt{x}+2}{\sqrt{x}+1}\right):\dfrac{x+1+2\sqrt{x}}{x-1}\left(dk:x>0,x\ne1\right)\)
\(=\left(\dfrac{\left(\sqrt{x}-1\right)^2}{\sqrt{x}-1}+\dfrac{2\left(\sqrt{x}+1\right)}{\sqrt{x}+1}\right):\dfrac{\left(\sqrt{x}+1\right)^2}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\)
\(=\left(\sqrt{x}-1+2\right):\dfrac{\sqrt{x}+1}{\sqrt{x}-1}\)
\(=\left(\sqrt{x}+1\right).\dfrac{\sqrt{x}-1}{\sqrt{x}+1}\\ =\sqrt{x}-1\)
\(b,P< 0\Leftrightarrow\sqrt{x}-1< 0\Leftrightarrow\sqrt{x}< 1\Leftrightarrow x< 1\)
So với \(dk:x>0\) \(\Rightarrow S=\left\{x|0< x< 1\right\}\)
đk với x>0,x khác 1