Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a)
\(\begin{array}{l}\overrightarrow {AB} + \overrightarrow {BC} + \overrightarrow {CD} + \overrightarrow {DA} = \left( {\overrightarrow {AB} + \overrightarrow {BC} } \right) + \left( {\overrightarrow {CD} + \overrightarrow {DA} } \right)\\ = \overrightarrow {AC} + \overrightarrow {CA} = \overrightarrow {AA} = \overrightarrow 0 .\end{array}\)
b)
\(\overrightarrow {AC} - \overrightarrow {AD} = \overrightarrow {DC} \) và \(\overrightarrow {BC} - \overrightarrow {BD} = \overrightarrow {DC} \)
\( \Rightarrow \overrightarrow {AC} - \overrightarrow {AD} = \overrightarrow {BC} - \overrightarrow {BD} \)

\(\overrightarrow{AB}+\overrightarrow{CD}+\overrightarrow{BC}=\left(\overrightarrow{AB}+\overrightarrow{BC}\right)+\overrightarrow{CD}\)
\(=\overrightarrow{AC}+\overrightarrow{CD}=\overrightarrow{AD}\) (đpcm)

\(a\text{) }\overrightarrow{AB}-\overrightarrow{CD}=\left(\overrightarrow{AC}+\overrightarrow{CB}\right)-\overrightarrow{CD}\\ =\overrightarrow{AC}-\left(\overrightarrow{CD}-\overrightarrow{CB}\right)=\overrightarrow{AC}-\overrightarrow{BD}\)
\(b\text{) }\overrightarrow{AB}+\overrightarrow{DC}+\overrightarrow{BD}+\overrightarrow{CA}=\left(\overrightarrow{AB}+\overrightarrow{BD}\right)+\left(\overrightarrow{DC}+\overrightarrow{CA}\right)\\ =\left(\overrightarrow{AB}+\overrightarrow{BD}\right)+\left(\overrightarrow{DC}+\overrightarrow{CA}\right)=\overrightarrow{AD}+\overrightarrow{DA}=0\)
\(c\text{) }\overrightarrow{AC}+\overrightarrow{DE}-\overrightarrow{DC}-\overrightarrow{CE}+\overrightarrow{CB}\\ =\left(\overrightarrow{AC}+\overrightarrow{CB}\right)+\left(\overrightarrow{DE}-\overrightarrow{DC}\right)-\overrightarrow{CE}\\ =\overrightarrow{AB}+\overrightarrow{CE}-\overrightarrow{CE}=\overrightarrow{AB}\)
\(d\text{) }\overrightarrow{AB}+\overrightarrow{DE}+\overrightarrow{CF}\\ =\left(\overrightarrow{AC}+\overrightarrow{CB}\right)+\left(\overrightarrow{DF}+\overrightarrow{FE}\right)+\left(\overrightarrow{CE}+\overrightarrow{EF}\right)\\ =\overrightarrow{AC}+\overrightarrow{CE}+\overrightarrow{CB}+\overrightarrow{DF}+\left(\overrightarrow{FE}+\overrightarrow{EF}\right)\\ =\overrightarrow{AC}+\overrightarrow{CE}+\overrightarrow{CB}+\overrightarrow{DF}\)

a)
\(\begin{array}{l}\overrightarrow {AB} + \overrightarrow {CD} = \overrightarrow {AD} + \overrightarrow {CB} \\ \Leftrightarrow \overrightarrow {AB} - \overrightarrow {CB} = \overrightarrow {AD} - \overrightarrow {CD} \\ \Leftrightarrow \overrightarrow {AB} + \overrightarrow {BC} = \overrightarrow {AD} + \overrightarrow {DC} \\ \Leftrightarrow \overrightarrow {AC} = \overrightarrow {AC} \end{array}\)
(luôn đúng)
b) \(\overrightarrow {AB} + \overrightarrow {CD} + \overrightarrow {BC} + \overrightarrow {DA} = \overrightarrow 0 \)
Ta có:
\(\begin{array}{l}\overrightarrow {AB} + \overrightarrow {CD} + \overrightarrow {BC} + \overrightarrow {DA} = (\overrightarrow {AB} + \overrightarrow {BC} ) + (\overrightarrow {CD} + \overrightarrow {DA} )\\ = \overrightarrow {AC} + \overrightarrow {CA} = \overrightarrow 0 \end{array}\)
Chú ý khi giải
+) Hiệu hai vecto chung gốc: \(\overrightarrow {AB} - \overrightarrow {AC} = \overrightarrow {CB} \) (suy ra từ tổng \(\overrightarrow {AB} = \overrightarrow {AC} + \overrightarrow {CB} \))
+) Với 4 điểm A, B, C, D bất kì ta có: \(\overrightarrow {AB} + \overrightarrow {BC} + \overrightarrow {CD} + \overrightarrow {DA} = \overrightarrow {AA} = \overrightarrow 0 \)

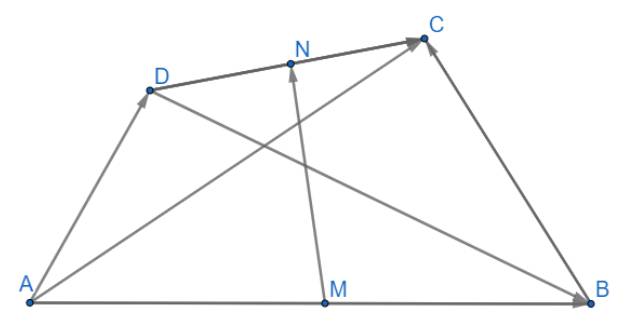
a) \(\overrightarrow {AC} + \overrightarrow {BD} = \overrightarrow {AM} + \overrightarrow {MN} + \overrightarrow {NC} + \overrightarrow {BM} + \overrightarrow {MN} + \overrightarrow {ND} \\= \left( {\overrightarrow {AM} + \overrightarrow {BM} } \right) + \left( {\overrightarrow {MN} + \overrightarrow {MN} } \right) + \left( {\overrightarrow {NC} + \overrightarrow {ND} } \right) \\= \overrightarrow 0 + 2\overrightarrow {MN} + \overrightarrow 0 = 2\overrightarrow {MN} \) (đpcm)
b) \(\overrightarrow {AC} + \overrightarrow {BD} = \overrightarrow {BC} + \overrightarrow {AD} \)
\(\)\(\overrightarrow {BC} + \overrightarrow {AD} = \overrightarrow {BM} + \overrightarrow {MN} + \overrightarrow {NC} + \overrightarrow {AM} + \overrightarrow {MN} + \overrightarrow {ND} \)
\(\left( {\overrightarrow {BM} + \overrightarrow {AM} } \right) + \left( {\overrightarrow {MN} + \overrightarrow {MN} } \right) + \left( {\overrightarrow {NC} + \overrightarrow {ND} } \right) = 2\overrightarrow {MN} \)
Mặt khác ta có: \(\overrightarrow {AC} + \overrightarrow {BD} = 2\overrightarrow {MN} \)
Suy ra \(\overrightarrow {AC} + \overrightarrow {BD} = \overrightarrow {BC} + \overrightarrow {AD} \)
Cách 2:
\(\begin{array}{l}
\overrightarrow {AC} + \overrightarrow {BD} = \overrightarrow {BC} + \overrightarrow {AD} \\
\Leftrightarrow \overrightarrow {AC} - \overrightarrow {AD} = \overrightarrow {BC} - \overrightarrow {BD} \\
\Leftrightarrow \overrightarrow {DC} = \overrightarrow {DC} (đpcm)
\end{array}\)

a.\(\overrightarrow{AB}+\overrightarrow{CD}=\overrightarrow{AD}+\overrightarrow{CB}\)
VT:\(\overrightarrow{AB}+\overrightarrow{CD}\)
=\(\overrightarrow{AC}+\overrightarrow{CB}+\overrightarrow{CA}+\overrightarrow{AD}\)
=\(\overrightarrow{AB}+\overrightarrow{CB}=0\left(đpcm\right)\)
b.\(\overrightarrow{AB}+\overrightarrow{CD}+\overrightarrow{EA}=\overrightarrow{ED}+\overrightarrow{CB}\)
\(\Leftrightarrow\overrightarrow{AB}+\overrightarrow{CD}+\overrightarrow{EA}+\overrightarrow{DE}+\overrightarrow{BC}=\overrightarrow{0}\)
\(\Leftrightarrow\overrightarrow{AC}+\overrightarrow{CE}+\overrightarrow{EA}=\overrightarrow{0}\)
\(\Leftrightarrow\overrightarrow{AE}+\overrightarrow{EA}=\overrightarrow{0}\)
\(\Leftrightarrow\overrightarrow{0}=\overrightarrow{0}\left(LĐ\right)\)

Với 4 điểm A, B, C, D ta có: \(\overrightarrow {AB} = \overrightarrow {CD} \) khi và chỉ khi tứ giác ABDC là hình bình hành
Theo tính chất của hình bình hành thì giao điểm của hai đường chéo là trung điểm của mỗi đường và ngược lại.
Nói cách khác: trung điểm của hai đoạn thẳng AD và BC trùng nhau.
Vậy ta có điều phải chứng minh.
Với 4 điểm A, B, C, D ta có: \(\overrightarrow {AB} = \overrightarrow {CD} \) khi và chỉ khi tứ giác ABDC là hình bình hành
Theo tính chất của hình bình hành thì giao điểm của hai đường chéo là trung điểm của mỗi đường và ngược lại.
Nói cách khác: trung điểm của hai đoạn thẳng AD và BC trùng nhau.
Vậy ta có điều phải chứng minh.

\(\overrightarrow{AB}+\overrightarrow{CD}=\overrightarrow{AB}+\overrightarrow{CB}+\overrightarrow{BD}=\overrightarrow{AB}+\overrightarrow{BD}+\overrightarrow{CB}=\overrightarrow{AD}+\overrightarrow{CB}\)
\(\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}+\overrightarrow{OD}=\left(\overrightarrow{OE}+\overrightarrow{EA}\right)+\left(\overrightarrow{OF}+\overrightarrow{FB}\right)+\left(\overrightarrow{OE}+\overrightarrow{EC}\right)+\left(\overrightarrow{OF}+\overrightarrow{FD}\right)\)
\(=2\left(\overrightarrow{OE}+\overrightarrow{EF}\right)+\left(\overrightarrow{EA}+\overrightarrow{EC}\right)+\left(\overrightarrow{FB}+\overrightarrow{FD}\right)\)
\(=2.\overrightarrow{0}+\overrightarrow{0}+\overrightarrow{0}=\overrightarrow{0}\)
Giả sử \(\overrightarrow{AB}-\overrightarrow{CD}=\overrightarrow{AC}-\overrightarrow{BD}\)
\(\Leftrightarrow\overrightarrow{AB}+\overrightarrow{DC}-\overrightarrow{AC}+\overrightarrow{BD}=\overrightarrow{0}\)
\(\Leftrightarrow\left(\overrightarrow{AB}+\overrightarrow{BD}\right)+\left(\overrightarrow{DC}-\overrightarrow{AC}\right)=\overrightarrow{0}\)
\(\Leftrightarrow\overrightarrow{AD}+\overrightarrow{DA}=\overrightarrow{0}\).
Vậy điều giả sử đúng. Ta có điều phải chứng minh.