Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi số cần tìm có dạng là \(\overline{X9}\)
Theo đề, ta có: \(\overline{9X}-\overline{X9}=2889\)
=>9000+X-10X-9=2889
=>-9X=-6102
=>X=678
=>Số cần tìm là 6789

1) Số chính phương (bình phương của 1 số) có chữ số tận cùng là 0; 5; ....
Vậy chỉ xét những số có tận cùng là 5 và 0 là : 2305; 2035; 3205; 3052; 2350; 2530; 3250; 3025
Trong các số trên chỉ có số 3025 là số chính phương; mà 3025 = 552
Số cần tìm là 55
2) và 3) tương tự

Gọi số đã cho là \(\overline{abc9}\)( \(0< a\le9\); \(0\le b,c\le9\))
Nếu chuyển chữ số hàng đơn vị lên đầu ta được: \(\overline{9abc}\)
Ta có: \(\overline{9abc}-\overline{abc9}=2889\)
\(\Rightarrow9000+100a+10b+c-\left(1000a+100b+10c+9\right)=2889\)
\(\Rightarrow9000+100a+10b+c-1000a-100b-10c-9=2889\)
\(\Rightarrow1000a+100b+10c-100a-10b-c=9000-9-2889\)
\(\Rightarrow900a+90b+9c=6102\)\(\Rightarrow100a+10b+c=678\)
hay \(\overline{abc}=678\)
Vậy số đã cho là \(6789\)

Giả sử a > b > c > d
Khi đó ta có số tự nhiên lớn nhất là \(\overline{abcd}\) và số tự nhiên nhỏ nhất là \(\overline{dcba}\)
=> \(\overline{abcd}+\overline{dcba}=11330\)
=> Ta có : \(a+d=10;b+c=12\)
Vậy \(a+b+c+d=10+12=22\)
Bài 4:
Gọi số tự nhiên cần là abc3 :
Khi đó nếu bỏ chữ số tận cùng thì số mới là abc
Ta có:
abc3 - abc = (1000a + 100b + 10c + 3) - (100a + 10b + c)
=> 900a + 90b + 9c + 3=1992
=> 900a + 90b + 9c=1989
=> 9(100a + 10b + c)=1989
=> 100a + 10b + c = 221
=> abc = 221
=> abc3 = 2213
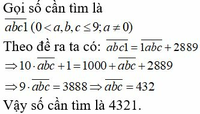
Câu đầu tiên mình không hiểu đề cho lắm . Đôi một khác nhau và khác 0 ???
b ) Gọi số cần tìm là abc9
9bca - abc9 = 2889
( 9000 + 100b + 10c + a ) - ( 1000a + 100b + 10c + 9 ) = 2889
( 9000 + a ) - ( 1000a + 9 ) = 2889
8991 - 999a = 2889
=> 999a = 6102
Bạn xem lại đề nhé .