Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A
Phương pháp: Chia cả 2 vế cho 3x, đặt  , tìm điều kiện của t.
, tìm điều kiện của t.
Đưa về bất phương trình dạng ![]()
Cách giải :
![]()

Ta có 

Đặt  , khi đó phương trình trở thành
, khi đó phương trình trở thành
![]()

![]()
![]()
![]()
![]()
Ta có: 



Vậy 

Có ![]()
![]()
Đặt t=f(x)+m bất phương trình trở thành: ![]()
![]()
Vậy ![]()
![]()
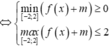
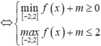
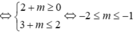
Chọn đáp án B.

Để bất phương trình nghiệm đúng với mọi x trước tiên bất phương trình phải xác định trên R.
Tức
![]()
![]()

Khi đó yêu cầu bài toán tương đương với:
![]()
![]()
![]()
Ta luôn có ![]() .
.
Xét ![]()
 Vậy khi
m
≤
-
1
4
thì điều này không xảy ra, tức với mọi
m
≤
-
1
4
thì
Vậy khi
m
≤
-
1
4
thì điều này không xảy ra, tức với mọi
m
≤
-
1
4
thì ![]() Vậy các giá trị cần tìm là
m
≤
-
1
4
Vậy các giá trị cần tìm là
m
≤
-
1
4
Chọn đáp án C.

Đáp án D
Ta có : y = 3 sin 2 x + cos 2 x sin 2 x + 4 cos 2 x + 1 = 3 sin 2 x + cos 2 x sin 2 x + 2 cos 2 x + 3
và sin 2 x + 2 cos 2 x + 3 > 0 ; ∀ x ∈ ℝ
xét phương trình
y = 3 sin 2 x + cos 2 x sin 2 x + 2 cos 2 x + 3
⇔ sin 2 x + 2 cos 2 x + 3 y = 3 sin 2 x + cos 2 x ⇔ y − 3 sin 2 x + 2 y − 1 cos 2 x = − 3 y
Phương trình trên có nghiệm nên
y − 3 2 + 2 y − 1 2 ≥ − 3 y 2 ⇔ 5 y 2 − 10 y + 10 ≥ 9 y 2
⇔ − 4 y 2 − 10 y + 10 ≥ 0 ⇔ − 5 − 65 4 ≤ y ≤ − 5 + 65 4
Suy ra giá trị lớn nhất của y là − 5 + 65 4
Phương trình 3 sin 2 x + cos 2 x sin 2 x + 2 cos 2 x + 3 ≤ m + 1 nghiệm đúngg với mọi số thực x khi
− 5 + 65 4 ≤ m + 1 ⇔ m ≥ − 9 + 65 4

Đáp án D
Ta có :
y = 3 sin 2 x + cos 2 x sin 2 x + 4 cos 2 x + 1 = 3 sin 2 x + cos 2 x sin 2 x + 2 cos 2 x + 3
Và sin 2 x + 2 cos 2 x + 3 > 0 ; ∀ x ∈ ℝ .
xét phương trình y = 3 sin 2 x + cos 2 x sin 2 x + 2 cos 2 x + 3
⇔ sin 2 x + 2 cos 2 x + 3 y = 3 sin 2 x + cos 2 x ⇔ y − 3 sin 2 x + 2 y − 1 cos 2 x = − 3 y
Phương trình trên có nghiệm nên
y − 3 2 + 2 y − 1 2 ≥ − 3 y 2 ⇔ 5 y 2 − 10 y + 10 ≥ 9 y 2
⇔ − 4 y 2 − 10 y + 10 ≥ 0 ⇔ − 5 − 65 4 ≤ y ≤ − 5 + 65 4
Suy ra giá trị lớn nhất của y là − 5 + 65 4
Phương trình 3 sin 2 x + cos 2 x sin 2 x + 2 cos 2 x + 3 ≤ m + 1 nghiệm đúngg với mọi số thực x khi − 5 + 65 4 ≤ m + 1 ⇔ m ≥ − 9 + 65 4

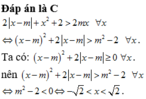


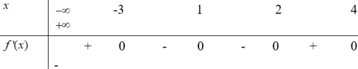
Đáp án C
Đặt t = 2 x 2 − 2 x , t ∈ 0 ; + ∞ ⇒ B P T ⇔ 2 t + t ≥ m 1
Ta có t + 2 t ≥ 2 t . 2 t = 2 2 ⇒ 1 ⇔ m ≤ 2 2