Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Áp dụng bđt Schwarz ta có:
\(P=\dfrac{a^4}{2ab+3ac}+\dfrac{b^4}{2cb+3ab}+\dfrac{c^4}{2ac+3bc}\ge\dfrac{\left(a^2+b^2+c^2\right)^2}{5\left(ab+bc+ca\right)}\ge\dfrac{\left(a^2+b^2+c^2\right)^2}{5\left(a^2+b^2+c^2\right)}=\dfrac{1}{5}\).
Đẳng thức xảy ra khi và chỉ khi \(a=b=c=\dfrac{\sqrt{3}}{3}\).

\(\dfrac{a^5}{b^3+c^2}+\dfrac{b^3+c^2}{4}+\dfrac{a^4}{2}\ge3\sqrt[3]{\dfrac{a^9.\left(b^3+c^2\right)}{8\left(b^3+c^2\right)}}=\dfrac{3a^3}{2}\)
Tương tự và cộng lại:
\(\Rightarrow M-\dfrac{a^4+b^4+c^4}{2}+\dfrac{a^3+b^3+c^3}{4}+\dfrac{a^2+b^2+c^2}{4}\ge\dfrac{3}{2}\left(a^3+b^3+c^3\right)\)
\(\Rightarrow M\ge\dfrac{a^4+b^4+c^4}{2}+\dfrac{5}{4}\left(a^3+b^3+c^3\right)-\dfrac{3}{4}\)
Mặt khác ta có:
\(\dfrac{1}{2}\left(a^4+b^4+c^4\right)\ge\dfrac{1}{6}\left(a^2+b^2+c^2\right)^2=\dfrac{3}{2}\)
\(\left(a^3+a^3+1\right)+\left(b^3+b^3+1\right)+\left(c^3+c^3+1\right)\ge3\left(a^2+b^2+c^2\right)=9\)
\(\Rightarrow2\left(a^3+b^3+c^3\right)+3\ge9\Rightarrow a^3+b^3+c^3\ge3\)
\(\Rightarrow M\ge\dfrac{3}{2}+\dfrac{15}{4}-\dfrac{3}{4}=...\)

Áp dụng BĐT Holder:
\(\left(\dfrac{a^2}{b+c}+\dfrac{b^2}{c+a}+\dfrac{c^2}{a+b}\right)^2\left[a^2\left(b+c\right)^2+b^2\left(c+a\right)^2+c^2\left(a+b\right)^2\right]\ge\left(a^2+b^2+c^2\right)^3\)
Mặt khác:
\(\left(a^2+b^2+c^2\right)^2\ge3\left(a^2b^2+b^2c^2+c^2a^2\right)\ge\dfrac{3}{2}\left(a^2b^2+b^2c^2+c^2a^2+abc\left(a+b+c\right)\right)\)
\(\Rightarrow\left(a^2+b^2+c^2\right)^2\ge\dfrac{3}{4}\left[a^2\left(b+c\right)^2+b^2\left(c+a\right)^2+c^2\left(a+b\right)^2\right]\)
\(\Rightarrow\left(\dfrac{a^2}{b+c}+\dfrac{b^2}{c+a}+\dfrac{c^2}{a+b}\right)^2\ge\dfrac{3}{4}\left(a^2+b^2+c^2\right)\)
\(\Rightarrow\dfrac{a^2}{b+c}+\dfrac{b^2}{c+a}+\dfrac{c^2}{a+b}\ge\dfrac{\sqrt{3}}{2}\sqrt{a^2+b^2+c^2}\)
\(\Rightarrow P\ge\dfrac{\sqrt{3}}{2}\sqrt{a^2+b^2+c^2}+\dfrac{4}{\sqrt{a^2+b^2+c^2+1}}\)
Đặt \(\sqrt{\dfrac{a^2+b^2+c^2}{3}}=x>0\)
\(\Rightarrow P\ge\dfrac{3x}{2}+\dfrac{4}{\sqrt{3x^2+1}}\)
Ta sẽ chứng minh \(P\ge\dfrac{7}{2}\)
Thật vậy, với \(x\ge\dfrac{7}{3}\Rightarrow P>\dfrac{3x}{2}\ge\dfrac{7}{2}\) (đúng)
Với \(0< x\le\dfrac{7}{3}\) ta cần chứng minh:
\(\dfrac{3x}{2}+\dfrac{4}{\sqrt{3x^2+1}}\ge\dfrac{7}{2}\Leftrightarrow\dfrac{4}{\sqrt{3x^2+1}}\ge\dfrac{7-3x}{2}\)
\(\Leftrightarrow64\ge\left(7-3x\right)^2\left(3x^2+1\right)\)
\(\Leftrightarrow3\left(x-1\right)^2\left(-9x^2+24x+5\right)\ge0\)
\(\Leftrightarrow\left(x-1\right)^2\left[3x\left(7-3x\right)+3x+5\right]\ge0\) (đúng)
Vậy \(P_{min}=\dfrac{7}{2}\) khi \(x=1\) hay \(a=b=c=1\)

\(VT=\sqrt{\dfrac{a^2b^2}{c\left(a+b+c\right)+ab}}+\sqrt{\dfrac{b^2c^2}{a\left(a+b+c\right)+bc}}+\sqrt{\dfrac{a^2c^2}{b\left(a+b+c\right)+ac}}\\ VT=\sqrt{\dfrac{a^2b^2}{ac+ab+bc+c^2}}+\sqrt{\dfrac{b^2c^2}{a^2+ac+ab+bc}}+\sqrt{\dfrac{a^2c^2}{ab+bc+b^2+ac}}\\ VT=\sqrt{\dfrac{a^2b^2}{\left(c+a\right)\left(b+c\right)}}+\sqrt{\dfrac{a^2c^2}{\left(b+c\right)\left(a+b\right)}}+\sqrt{\dfrac{b^2c^2}{\left(a+b\right)\left(a+c\right)}}\)
Áp dụng BĐT Cauchy-Schwarz:
\(\Leftrightarrow\left\{{}\begin{matrix}\sqrt{\dfrac{b^2c^2}{\left(a+b\right)\left(a+c\right)}}\le\dfrac{\dfrac{bc}{a+b}+\dfrac{bc}{a+c}}{2}\\\sqrt{\dfrac{a^2c^2}{\left(a+b\right)\left(b+c\right)}}\le\dfrac{\dfrac{ca}{a+b}+\dfrac{ca}{b+c}}{2}\\\sqrt{\dfrac{a^2b^2}{\left(b+c\right)\left(a+c\right)}}\le\dfrac{\dfrac{ab}{b+c}+\dfrac{ab}{a+c}}{2}\end{matrix}\right.\)
\(\Rightarrow VT\le\dfrac{\left(\dfrac{bc}{a+b}+\dfrac{ca}{a+b}\right)+\left(\dfrac{ca}{b+c}+\dfrac{ab}{b+c}\right)+\left(\dfrac{bc}{a+c}+\dfrac{ab}{a+c}\right)}{2}\\ \Rightarrow VT\le\dfrac{a+b+c}{2}=\dfrac{2}{2}=1\)
Dấu \("="\Leftrightarrow a=b=c=\dfrac{2}{3}\)

\(4\left(a+b+c\right)=a^2+\left(b+c\right)^2\ge\dfrac{1}{2}\left(a+b+c\right)^2\)
\(\Rightarrow a+b+c\le8\)
\(a^2+16-16\ge8a-16\)
\(\Rightarrow P\ge8\left(a+b+c\right)-16+\dfrac{8100}{\sqrt{2a+2b+1}+\sqrt{2c+1}}\)
\(\Rightarrow P\ge8\left(a+b+c\right)-16+\dfrac{48600}{6\sqrt{2a+2b+1}+6\sqrt{2c+1}}\)
\(\Rightarrow P\ge8\left(a+b+c\right)-16+\dfrac{24300}{a+b+c+10}\)
\(\Rightarrow P\ge8\left(a+b+c+10+\dfrac{324}{a+b+c+10}\right)+\dfrac{21708}{a+b+c+10}-96\)
\(\Rightarrow P\ge16.\sqrt{324}+\dfrac{21708}{18}-96=1398\)
Dấu "=" xảy ra tại \(\left(a;b;c\right)=\left(4;0;4\right)\)

Ta có: \(a^2+b^2+c^2\ge ab+bc+ca\ge\sqrt[]{abc}\left(\sqrt{a}+\sqrt{b}+\sqrt{c}\right)\)
Do đó:
\(VT\le\dfrac{2a^3}{2\sqrt{a^6bc}}+\dfrac{2b^3}{2\sqrt{b^6ac}}+\dfrac{2c^3}{2\sqrt{c^3ab}}=\dfrac{\sqrt{a}+\sqrt{b}+\sqrt{c}}{\sqrt{abc}}=\dfrac{\sqrt{abc}\left(\sqrt{a}+\sqrt{b}+\sqrt{c}\right)}{abc}\)
\(\le\dfrac{a^2+b^2+c^2}{abc}=\dfrac{a}{bc}+\dfrac{b}{ca}+\dfrac{c}{ab}\)
Dấu "=" xảy ra khi \(a=b=c=1\)

Bạn xem lại đề, với a;b;c dương thì biểu thức P không tồn tại max nếu đề hoàn toàn đúng
Muốn P tồn tại max thì a;b;c cần không âm (nghĩa là có thể bằng 0)
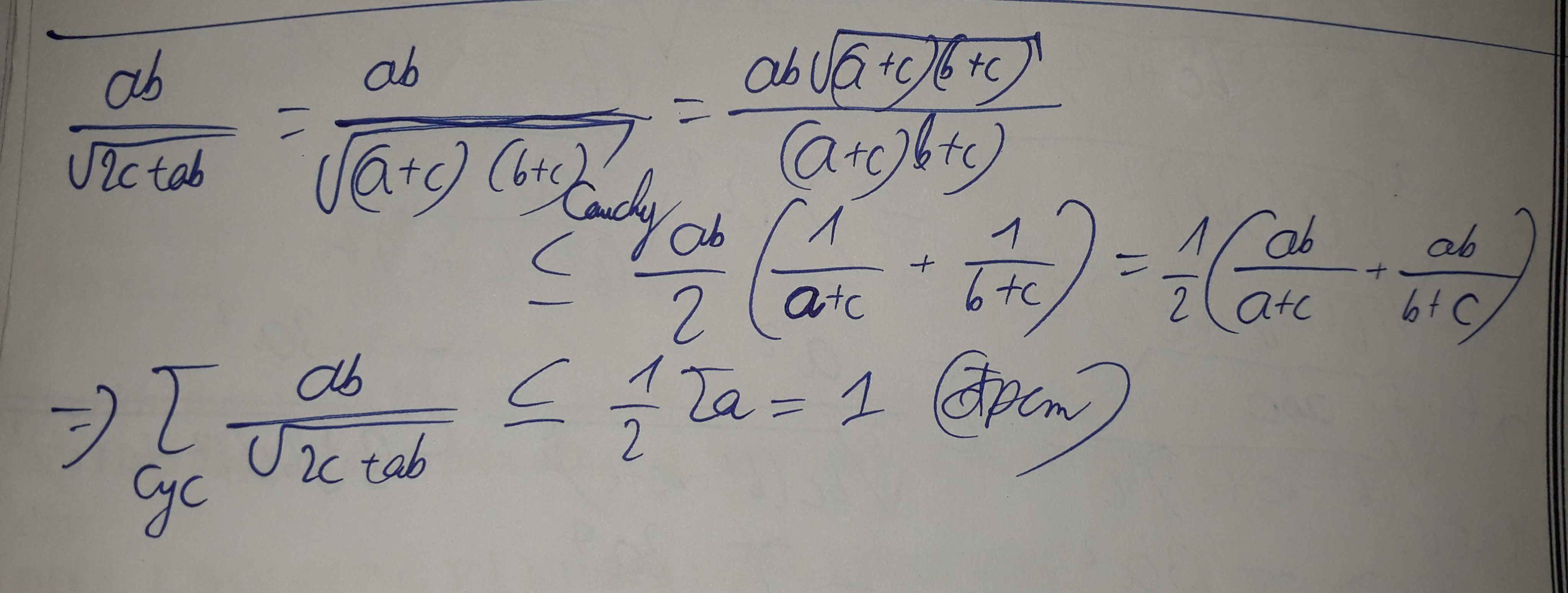
bạn đố thế ai chơi