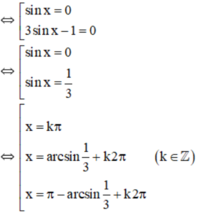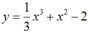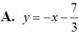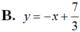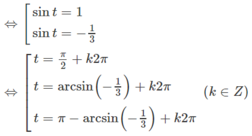Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn A.
Ta có y’ = x2 + 2x và y” = 2x + 2
Theo giả thiết xo là nghiệm của phương trình y”(xo) = 0
⇔ 2x + 2 = 0 ⇔ xo = -1
Và y’(-1) = -1
Phương trình tiếp tuyến tại điểm 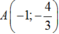 là: y = -1.(x + 1) - 7/3
là: y = -1.(x + 1) - 7/3
Hay  .
.

Ta có y ' = x 2 + 2 x và y" = 2x + 2.
- Theo giả thiết x 0 là nghiệm của phương trình y " ( x 0 ) = 0 .
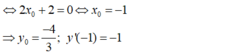
- Phương trình tiếp tuyến tại điểm 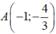 là:
là:
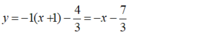
Chọn A.

- Ta có :
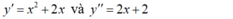
- Theo giả thiết x 0 là nghiệm của phương trình:
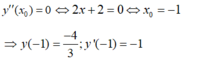
- Phương trình tiếp tuyến tại điểm 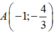 là:
là:
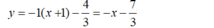
Chọn A.

Câu 1:
Đặt \(f\left(x\right)=x^3+mx^2+\left(m-3\right)x-1\)
Ta có \(f\left(0\right)=-1\) ; \(f\left(-1\right)=1\)
\(\Rightarrow f\left(0\right).f\left(-1\right)< 0\Rightarrow f\left(x\right)\) có ít nhất 1 nghiệm thuộc \(\left(-1;0\right)\)
Mặt khác \(\left\{{}\begin{matrix}f\left(0\right)=-1< 0\\\lim\limits_{x\rightarrow+\infty}=+\infty\end{matrix}\right.\) \(\Rightarrow f\left(x\right)\) có ít nhất 1 nghiệm thuộc \(\left(0;+\infty\right)\)
\(\left\{{}\begin{matrix}f\left(-1\right)=1>0\\\lim\limits_{x\rightarrow-\infty}=-\infty\end{matrix}\right.\) \(\Rightarrow f\left(x\right)\) có ít nhất 1 nghiệm thuộc \(\left(-\infty;-1\right)\)
Vậy pt đã cho có 3 nghiệm phân biệt với mọi m
Câu 2:
\(f'\left(x\right)=x^2+2\left(m-1\right)x+m+1\)
Để \(f'\left(x\right)\ge0\) \(\forall x\) \(\Leftrightarrow\Delta'=\left(m-1\right)^2-\left(m+1\right)\le0\)
\(\Leftrightarrow m^2-3m\le0\Leftrightarrow0\le m\le3\)
Câu 3:
Nhận thấy \(x=0\) không phải nghiệm
\(\Leftrightarrow2x^3+3x^2-2=-mx\)
\(\Leftrightarrow\frac{2x^3+3x^2-2}{x}=-m\)
Đặt \(f\left(x\right)=\frac{2x^3+3x^2-2}{x}\Rightarrow f'\left(x\right)=\frac{\left(6x^2+6x\right)x-\left(2x^3+3x^2-2\right)}{x^2}=\frac{4x^3+3x^2+2}{x^2}\)
\(f'\left(x\right)=\frac{4x^2\left(x+1\right)+2-x^2}{x^2}\Rightarrow f'\left(x\right)>0\) \(\forall x\in\left(-1;1\right)\)
\(\Rightarrow f\left(x\right)\) đồng biến trên \(\left(-1;1\right)\)
\(\lim\limits_{x\rightarrow0^-}f\left(x\right)=+\infty\) ; \(\lim\limits_{x\rightarrow0^+}f\left(x\right)=-\infty\)
\(\Rightarrow y=-m\) luôn cắt đồ thị \(y=f\left(x\right)\) hay phương trình đã cho luôn có ít nhất 1 nghiệm trong khoảng \(\left(-1;1\right)\) với mọi m

a.
\(u_5=18\Rightarrow u_1+4d=18\) (1)
\(4S_n=S_{2n}\Rightarrow\dfrac{4n\left(2u_1+\left(n-1\right)d\right)}{2}=\dfrac{2n\left(2u_1+\left(2n-1\right)d\right)}{2}\)
\(\Rightarrow4u_1+2\left(n-1\right)d=2u_1+\left(2n-1\right)d\)
\(\Rightarrow2u_1-d=0\Rightarrow d=2u_1\) (2)
Thế (2) vào (1):
\(\Rightarrow9u_1=18\Rightarrow u_1=2\Rightarrow d=4\)
b.
Do a;b;c là 3 số hạng liên tiếp của 1 CSC công sai 2 nên: \(\left\{{}\begin{matrix}b=a+2\\c=a+4\end{matrix}\right.\)
Khi tăng số thứ nhất thêm 1, số thứ 2 thêm 1 và số thứ 3 thêm 3 được 1 cấp số nhân nên:
\(\left(a+1\right)\left(c+3\right)=\left(b+1\right)^2\)
\(\Rightarrow\left(a+1\right)\left(a+7\right)=\left(a+3\right)^2\)
\(\Rightarrow a^2+8a+7=a^2+6a+9\)
\(\Rightarrow a=1\Rightarrow b=3\Rightarrow c=5\)

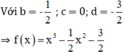
a) f’(x) = 3x2 – x.
⇒ f’(-1) = 4; f(-1) = -3.
⇒ Phương trình tiếp tuyến của đồ thị hàm số tại điểm có hoành độ x = -1 là:
y = 4.(x + 1) – 3 = 4x + 1.
b) f’(sin x) = 0
⇔ 3.sin2x – sin x = 0
⇔ sin x.(3sin x – 1) = 0