Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Để B có giá trị nguyên thì 5 \(⋮\sqrt{x}-1\) \(\Rightarrow\sqrt{x}-1\inƯ\left(5\right)\) \(\Rightarrow\sqrt{x}-1\in\left\{1;-1;5;-5\right\}\)
Ta có bảng:
| \(\sqrt{x}-1\) | 1 | -1 | 5 | -5 |
| \(x\) | 4 | 0 | 36 | 16 |
Vậy \(x\in\left\{4;0;36;16\right\}\)
Để phân số \(B=\dfrac{5}{\sqrt{x}-1}\) có giá trị nguyên thì: \(5⋮\sqrt{x}-1\\ \Rightarrow\sqrt{x}-1\inƯ\left(5\right)\\ \Rightarrow\sqrt{x}-1\in\left\{\pm1;\pm5\right\}\)
Ta lập bảng sau:
| \(\sqrt{x}-1\) | 1 | -1 | 5 | -5 |
| \(x\) | 4 | 0 | 36 | 16 |
Vậy \(x\in\left\{4;0;36;16\right\}\).


Để A nguyên thì \(\sqrt{x}-3⋮2\)
Do x < 30 nên \(\sqrt{x}< 6\) => \(\sqrt{x}-3< 3\)
Lại có: \(\sqrt{x}-3\ge-3\) do \(\sqrt{x}\ge0\)
=> \(\sqrt{x}-3\in\left\{2;0;-2\right\}\)
\(\Rightarrow\sqrt{x}\in\left\{5;3;1\right\}\)
\(\Rightarrow x\in\left\{25;9;1\right\}\)
Vậy ...

a: Sửa đề: \(A=\dfrac{\sqrt{x}+1}{\sqrt{x}-3}\)
ĐKXĐ: \(\left\{{}\begin{matrix}x>=0\\x\ne9\end{matrix}\right.\)
Để A là số nguyên thì \(\sqrt{x}+1⋮\sqrt{x}-3\)
=>\(\sqrt{x}-3+4⋮\sqrt{x}-3\)
=>\(4⋮\sqrt{x}-3\)
=>\(\sqrt{x}-3\in\left\{1;-1;2;-2;4;-4\right\}\)
=>\(\sqrt{x}\in\left\{4;2;5;1;7;-1\right\}\)
=>\(\sqrt{x}\in\left\{4;2;5;1;7\right\}\)
=>\(x\in\left\{16;4;25;1;49\right\}\)
b: 
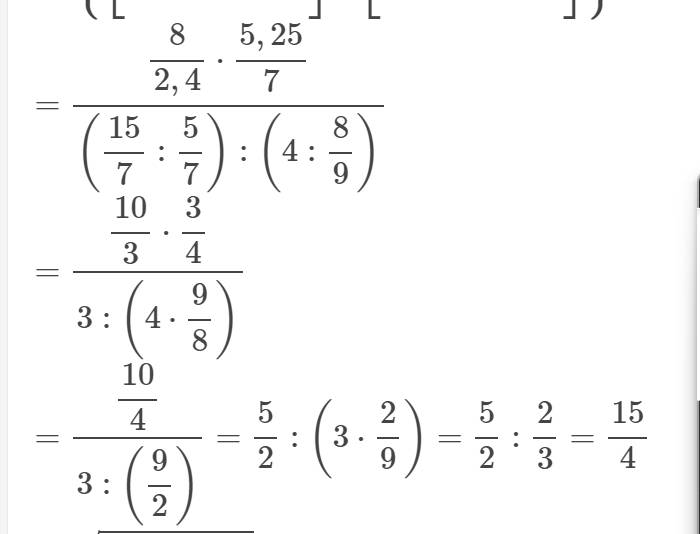

Để A có giá trị là một số nguyên thì:
\(\left(\sqrt{x}+1\right)⋮\left(\sqrt{x}-3\right)\)
\(\Leftrightarrow\left(\sqrt{x}-3\right)+4⋮\left(\sqrt{x}-3\right)\)
\(\Leftrightarrow4⋮\left(\sqrt{x}-3\right)\)
Vì \(x\in Z\) nên \(\left(\sqrt{x}-3\right)\inƯ\left(4\right)=\left\{\pm1,\pm2,\pm4\right\}\)
Ta có bảng sau:
| \(\sqrt{x}-3\) | 1 | -1 | 2 | -2 | 4 | -4 |
| \(\sqrt{x}\) | 4 | 2 | 5 | 1 | 7 | -1 |
| x | 16 | 4 | 25 | 1 | 49 | (loại) |
Vậy ....
Ta có: \(A=\dfrac{\sqrt{x}+1}{\sqrt{x}-3}=\dfrac{\left(\sqrt{x}-3\right)+4}{\sqrt{x}-3}=\dfrac{\sqrt{x}-3}{\sqrt{x}-3}=\dfrac{4}{\sqrt{x}-3}=1+\dfrac{4}{\sqrt{x}-3}\)
Để A có giá trị là một số nguyên khi:
\(4⋮\sqrt{x}-3\) hay \(\sqrt{x}-3\inƯ\left(4\right)=\left\{\pm1;\pm2;\pm4\right\}\)
Do đó:
\(\sqrt{x}-3=-1\Rightarrow\sqrt{x}=-1+3=2\Rightarrow x=4\)
\(\sqrt{x}-3=1\Rightarrow\sqrt{x}=1+3=4\Rightarrow x=16\)
\(\sqrt{x}-3=-2\Rightarrow\sqrt{x}=-2+3=1\Rightarrow x=1\)
\(\sqrt{x}-3=2\Rightarrow\sqrt{x}=2+3=5\Rightarrow x=25\)
\(\sqrt{x}-3=-4\Rightarrow\sqrt{x}=-4+3=-1\) ( loại )
\(\sqrt{x}-3=4\Rightarrow\sqrt{x}=4+3=7\Rightarrow x=49\)
Vậy để A là một số nguyên khi \(x\in\left\{4;16;1;25;49\right\}\)

Để A nguyên thì \(\sqrt{x-3}\) chia hết cho 2
Vì x < 30 => x - 3 < 27 => \(\sqrt{x-3}

\(A=\dfrac{\sqrt{x}-3}{2}\) có giá trị nguyên nên \(\left(\sqrt{x}-3\right)⋮2.\)
Suy ra \(x\) là số chính phương lẻ.
Vì \(x< 30\) nên \(x\in\left\{1^2;3^2;5^2\right\}\)hay \(x\in\left\{1;9;25\right\}.\)