Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đặt BH=x; CH=y
Theo đề, ta có: x+y=25 và xy=144
=>x,y là các nghiệm của phương trình là;
a^2-25a+144=0
=>a=9 hoặc a=16
TH1: BH=9; CH=16
AB=căn 9*25=15cm
AC=căn 16*20=20cm
TH2: BH=16; CH=9
AB=căn 16*25=20cm
AC=căn 9*25=15cm

Đặt BH=x; CH=y(x<y)
Theo đề, ta có:
x+y=25 và xy=12^2=144
=>x,y là các nghiệm của phương trình:
a^2-25a+144=0
=>a=9; a=16
=>BH=9cm; CH=16cm
AH=căn 9*16=12cm
AB=căn 9*25=15cm
AC=căn 16*25=20cm


a) \(AH^2=HB.HC=50.8=400\)
\(\Rightarrow AH=20\left(cm\right)\)
\(S_{ABC}=\dfrac{1}{2}AH.BC=\dfrac{1}{2}.20\left(50+8\right)=\dfrac{1}{2}.20.58\left(cm^2\right)\)
mà \(S_{ABC}=\dfrac{1}{2}AB.AC\)
\(\Rightarrow AB.AC=20.58=1160\)
Theo Pitago cho tam giác vuông ABC :
\(AB^2+AC^2=BC^2\)
\(\Rightarrow\left(AB+AC\right)^2-2AB.AC=BC^2\)
\(\Rightarrow\left(AB+AC\right)^2=BC^2+2AB.AC\)
\(\Rightarrow\left(AB+AC\right)^2=58^2+2.1160=5684\)
\(\Rightarrow AB+AC=\sqrt[]{5684}=2\sqrt[]{1421}\left(cm\right)\)
Chu vi Δ ABC :
\(AB+AC+BC=2\sqrt[]{1421}+58=2\left(\sqrt[]{1421}+29\right)\left(cm\right)\)

Gia sử: AB < AC => BH < HC
A B C H
Áp dụng hệ thức lượng ta có:
\(AH^2=BH.CH\)
\(\Rightarrow\)\(BH.CH=144\)
\(BH+CH=BC=25\)
Áp dụng hệ thức Vi-ét thì BH và CH là nghiệm của phương trình:
\(x^2-25x+144=0\)
\(\Leftrightarrow\)\(\left(x-9\right)\left(x-16\right)=0\)
\(\Leftrightarrow\)\(\orbr{\begin{cases}x=9\\x=16\end{cases}}\)
Do BH < HC (theo cách vẽ) nên \(BH=9;\)\(HC=16\)
Áp dụng hệ thức lượng ta có:
\(AB^2=BH.BC\)
\(\Rightarrow\)\(AB^2=9.25=225\)
\(\Rightarrow\)\(AB=15\)
\(AC^2=CH.BC\)
\(\Rightarrow\)\(AC^2=16.25=400\)
\(\Rightarrow\)\(AC=20\)

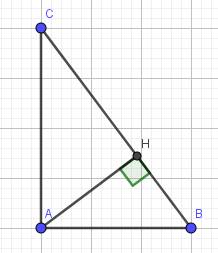
\(\Delta ABC\) vuông tại A, đường cao AH
\(\Rightarrow AH.BC=AB.AC\)
\(\Rightarrow AB=\dfrac{AH.BC}{AC}=\dfrac{12.25}{AC}=\dfrac{300}{AC}\)
Lại có:
\(AB^2+AC^2=BC^2=25^2=625\left(Pytago\right)\)
\(\Rightarrow\left(\dfrac{300}{AC}\right)^2+AC^2=625\)
\(\Leftrightarrow\dfrac{90000}{AC^2}+AC^2=625\)
\(\Leftrightarrow AC^4+90000=625AC^2\)
\(\Leftrightarrow AC^4-625AC^2+90000=0\)
\(\Leftrightarrow AC^4-225AC^2-400AC^2+90000=0\)
\(\Leftrightarrow\left(AC^4-225AC^2\right)-\left(400AC^2-90000\right)=0\)
\(\Leftrightarrow AC^2\left(AC^2-225\right)-400\left(AC^2-225\right)=0\)
\(\Leftrightarrow\left(AC^2-225\right)\left(AC^2-400\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}AC^2-225=0\\AC^2-400=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}AC^2=225\\AC^2=400\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}AC=15\\AC=20\end{matrix}\right.\)
*) \(AC=15cm\)
\(\Rightarrow AB=\dfrac{300}{15}=20\left(cm\right)\)
*) \(AC=20cm\)
\(\Rightarrow AB=\dfrac{300}{20}=15\left(cm\right)\)
Vậy AB = 20 cm; AC = 15 cm
Hoặc AB = 15 cm; AC = 20 cm

a) Xét tam giác ABH vuông tại H, ta có:
AB2 = AH2 + HB2 (ĐL Py-ta-go)
AB2 = 152 + 252
AB2 = 225 + 625
AB2 = 850
AB = \(\sqrt{850}\)(cm)
Xét tam giác ABC vuông tại A, có đường cao AH:
=> BA2 = BH.BC
850 = 25.BC
BC = 850:25
BC = 34
Xét tam giác ABC vuông tại A, ta có:
BC2 = AB2 + AC2
342 = 850 + AC2
1156 - 850 = AC2
AC2 = 306
AC = \(\sqrt{306}\)(cm)
Ta có BC = BH + HC
34 = 25 + HC
HC = 34 - 25
HC = 9
b) Xét tam giác ABH vuông tại H, ta có:
AB2 = AH2 + HB2 (ĐL Py-ta-go)
122 = AH2 + 62
144 = AH2 + 36
AH2 = 144 - 36
AH2 = 108
AH = \(\sqrt{108}\)(cm)
Xét tam giác ABC vuông tại A, có đường cao AH:
=> BA2 = BH.BC
122 = 6.BC
144 = 6.BC
BC = 144:6
BC = 24 (cm)
Ta có BC = BH + HC
24 = 6 + HC
HC = 24 - 6
HC = 18
Xét tam giác ABC vuông tại A, ta có:
BC2 = AB2 + AC2 (ĐL Py-ta-go)
242 = 122 + AC2
AC2 = 242 - 122
AC2 = 576 - 144
AC2 = 432
AC = \(\sqrt{432}\)(cm)

Đặt BH = x (0 < x < 25) (cm) => CH = 25 - x (cm)
Ta có : AH2=BH.CH⇒x(25−x)=144⇔x2−25x+144=0AH2=BH.CH⇒x(25−x)=144⇔x2−25x+144=0
(x−9)(x−16)=0(x−9)(x−16)=0 ⇔[x=9x=16⇔[x=9x=16 (tm)
Nếu BH = 9 cm thì CH = 16 cm⇒AB=√AH2+BH2=√92+122=15(cm)⇒AB=AH2+BH2=92+122=15(cm)
AC=√AH2+CH2=√122+162=20(cm)AC=AH2+CH2=122+162=20(cm)
Nếu BH = 16 cm thì CH = 9 cm
⇒AB=√AH2+BH2=√122+162=20(cm)⇒AB=AH2+BH2=122+162=20(cm)
AC=√AH2+CH2=√92+122=15(cm)
Theo đề, ta có:
\(HB\left(25-HB\right)=12^2=144\)
\(\Leftrightarrow HB^2-25HB+144=0\)
\(\Leftrightarrow\left(HB-9\right)\left(HB-16\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}HB=9\\HC=16\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}HC=16\\HC=9\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}AB=15\left(cm\right)\\AC=20\left(cm\right)\end{matrix}\right.\\\left\{{}\begin{matrix}AB=20\left(cm\right)\\AC=15\left(cm\right)\end{matrix}\right.\end{matrix}\right.\)