Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a.Áp dụng định lý pitago, ta có:
\(BC^2=AB^2+AC^2\)
\(\Rightarrow BC=\sqrt{6^2+8^2}=\sqrt{100}=10cm\)
b.AH: đã có
Áp dụng định lý pitago vào tam giác vuông AHC, có:
\(AC^2=AH^2+CH^2\)
\(\Rightarrow CH=\sqrt{AC^2-AH^2}=\sqrt{8^2-4,8^2}=\sqrt{40,96}=6,4cm\)

a) Diện tích tam giác ABC (Heron)
\(S_{ABC}=\frac{1}{4}\sqrt{\left(AB+BC+AC\right)\left(AB+BC-AC\right)\left(BC+AC-AB\right)\left(AC+AB-BC\right)}\)
\(S_{ABC}=\frac{1}{4}\sqrt{\left(6+10+8\right)\left(6+10-8\right)\left(10+8-6\right)\left(8+6-10\right)}=24\left(cm^2\right)\)
b)Xét tam giác ABC có
\(BC^2=10^2=100\left(cm\right)\)
\(AB^2+AC^2=6^2+8^2=100\left(cm\right)\)
Vì 100cm=100cm
\(\Rightarrow BC^2=AB^2+AC^2\)
=> Tam giác ABC vuông tại A
Xét diện tích tam giác ABC thường \(S_{ABCt}=\frac{AH.BC}{2}\left(1\right)\)
Xét diện tích tam giác ABC vuông \(S_{ABCv}=\frac{AC.AB}{2}\left(2\right)\)
Từ (1) và (2)
\(\Leftrightarrow AH.BC=AB.AC\)
\(\Leftrightarrow AH.10=8.6\Leftrightarrow AH=4,8\left(cm\right)\)
Xét tam giác ABH vuông tại H
\(\Rightarrow BH^2=AB^2-AH^2\left(PYTAGO\right)\)
\(\Rightarrow BH=\sqrt{AB^2-AH^2}\)
\(\Rightarrow BH=\sqrt{6^2-13,3^2}=3,6\left(cm\right)\)
Xét tam giác ACH vuông tại H
\(\Rightarrow HC^2=AC^2-AH^2\left(PYTAGO\right)\)
\(\Rightarrow HC=\sqrt{AC^2-AH^2}\)
\(\Rightarrow HC=\sqrt{8^2-4,8^2}=6,4\left(cm\right)\)

A B C H
AC
Áp dụng định lí Pytago cho tam giác vuông ABC ta có :
BC2 = AB2 + AC2
=> \(AC=\sqrt{BC^2-AB^2}=\sqrt{10^2-6^2}=8cm\)
AH
Đến đây đề thiếu dữ liệu
cho tam giác ABC vuông cân ở A, biết AB=6cm, AC=8cm, kẻ AH vuông góc với BC tại H. Tính AH, BH và HC

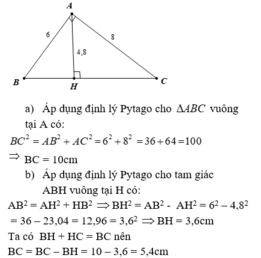
a: Xét ΔABC vuông tại A có
\(BC^2=AB^2+AC^2\)
nên BC=10(cm)
b: Xét ΔABH vuông tại H có \(AB^2=AH^2+HB^2\)
nên HB=3,6(cm)
=>HC=BC-HB=6,4(cm)
câu này lúc nãy làm rồi em nhé! ( bổ sung BH )
Áp dụng định lý pitago vào tam giác vuông ABH, có:
\(AB^2=BH^2+AH^2\)
\(\Rightarrow BH=\sqrt{AB^2-AH^2}=\sqrt{6^2-4,8^2}=\sqrt{12,96}=3,6cm\)