Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
a: Xét ΔABC vuông tại A có
\(BC^2=AB^2+AC^2\)
nên BC=10(cm)
b: Xét ΔABH vuông tại H có \(AB^2=AH^2+HB^2\)
nên HB=3,6(cm)
=>HC=BC-HB=6,4(cm)
câu này lúc nãy làm rồi em nhé! ( bổ sung BH )
Áp dụng định lý pitago vào tam giác vuông ABH, có:
\(AB^2=BH^2+AH^2\)
\(\Rightarrow BH=\sqrt{AB^2-AH^2}=\sqrt{6^2-4,8^2}=\sqrt{12,96}=3,6cm\)
a)
Áp dụng định lý pitago vào tam giác vuông ABC, có:
BC2=AB2+AC2BC2=AB2+AC2
⇒BC=√62+82=√100=10cm⇒BC=62+82=100=10cm
b.Xét tam giác vuông ABH và tam giác vuông ADH, có:
HD = HB ( gt )
AH: cạnh chung
Vậy tam giác vuông ABH = tam giác vuông ADH ( 2 cạnh góc vuông )
=> AB = AD ( 2 cạnh tương ứng )
bn tham khảo
a,Áp dụng Đ. L. py-ta-go, có:
BC2=AC2+AB2
=>BC2=82+62
=64+36.
=100.
=>BC=10cm.
b, Xét tg AHB và tg AHD, có:
AH chung
góc AHB= góc AHD(=90o)
HB= DH(gt)
=>tg AHB= tg AHD(2 cạnh góc vuông)
=>AB= AD(2 cạnh tương ứng)
c, Kẻ E với C, tạo thành cạnh EC.
Kẻ E với B, tạo thành cạnh EB.
Ta có: góc BHA=90o, suy ra: góc BHA= góc EHC(2 góc đối đỉnh)
=>góc BHA= góc EHC(=90o)
=>ED vuông góc với AC(đpcm)
a. Xét ΔABC vuông tại A, có:
AB2 + AC2 = BC2 (Định lý Py-ta-go)
⇒ 62 + 82 = BC2 (thay số)
⇒ BC2 = 100
⇒ BC = 10
b) Có: AH vuông góc với BC (gt)
⇒ góc AHB = góc AHD (tính chất ....)
Xét ΔAHB và ΔAHD, có:
BH = HD (gt)
góc AHB = AHD (cmt)
AH chung
⇒ ΔAHB = ΔAHD (c.g.c)
⇒ AB = AD (cặp cạnh tương ứng) (đpcm)
a, Áp dụng Đ. L. py-ta-go vào tg ABC vuông tạo A, có:
BC2=AC2+AB2.
=>BC2=82+62.
=64+36.
=100.
=>BC=10cm.
b, Vì góc BAC+ góc CAF=180o(kề bù)
=>góc CAF=180o-góc BAC
=180o-90o
=90o
Xét tg ABC và tg AFC, có:
AC chung
góc BAC= góc CAF(=90o)
AB=AF(gt)
=>tg ABC= tg AFC(c. g. c)
c, Vì tg ABC= tg AFC(cm câu b)
=>CF=CB(2 cạnh tương ứng)
=>tg CBF cân tại C.
d, Xét tg AHC và tg AKC, có:
góc HCA= góc KCA(2 góc tương ứng)
AC chung
góc AHC= góc AKC(2 góc tương ứng)
=>tg AHC= tg AKC(ch-gn)
=>CH=CK(2 cạnh tương ứng)
=>tg HKC cân tại C.
Ta có: tg HKC cân tại C, tg BFC cân tại C.
=> góc B= góc F= góc CHK= góc CKH.
Mà góc B và góc CHK ở vị trí đong vị, góc F và góc CKH cũng ở vị trí đồng vị.
=>BF//HK(đpcm)
AC
Áp dụng định lí Pytago cho tam giác vuông ABC ta có :
BC2 = AB2 + AC2
=> \(AC=\sqrt{BC^2-AB^2}=\sqrt{10^2-6^2}=8cm\)
AH
Đến đây đề thiếu dữ liệu
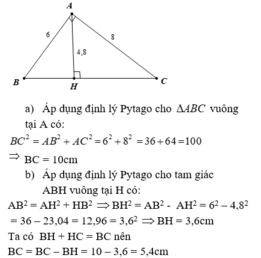
a.Áp dụng định lý pitago, ta có:
\(BC^2=AB^2+AC^2\)
\(\Rightarrow BC=\sqrt{6^2+8^2}=\sqrt{100}=10cm\)
b.AH: đã có
Áp dụng định lý pitago vào tam giác vuông AHC, có:
\(AC^2=AH^2+CH^2\)
\(\Rightarrow CH=\sqrt{AC^2-AH^2}=\sqrt{8^2-4,8^2}=\sqrt{40,96}=6,4cm\)
a)Xét tam giác ABC vuông có:
\(AB^2+AC^2=BC^2\\ 6^2+8^2=BC^2\\ BC^2=100\\ BC=10cm\)
b)Biết AH=4,8cm mà nó hỏi tính AH thì AH=4,8 (gt) =)?
Xét tam giác AHC vuông có:
\(AH^2+HC^2=AC^2\\ =>4,8^2+CH^2=8^2\\ =>CH^2=40,96\\ =>CH=6,4cm\)