Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: góc ABD=180-80=100 độ
góc BAD=180-100-30=50 độ
b: Xét ΔAIE và ΔBID có
IA=IB
góc AIE=góc BID
IE=ID
Do đó: ΔAIE=ΔBID
=>góc IAE=góc IBD
=>AE//BD
c: Xét tứ giác ABCE có
AE//BC
AE=BC
Do đó;ABCE là hình bình hành
=>CA cắt BE tại trung điểm của mỗi đường
=>K là trung điểm của AC

a: \(\widehat{BAD}=180^0-100^0-30^0=50^0\)
b: Xét ΔAIE và ΔBID có
IA=IB
\(\widehat{AIE}=\widehat{BID}\)
IE=ID
Do đo: ΔAIE=ΔBID
Xét tứ giác AEBD có
I là trung điểm của AB
I là trung điểm của DE
Do đó: AEBD là hình bình hành
Suy ra: AE//BD
c: Xét tứ giác ABCE có
AE//BC
AE=BC
Do đó: ABCE là hình bình hành
Suy ra: AC cắt BE tại trung điểm của mỗi đường
hay N là trung điểm của AC

Câu a thui
A, Xét Tam giác ABC và Tam giác AED có
AB=AD
BD cạnh chung
AC=AE
=>TAM GIÁC ABC=TAM GIÁC AED

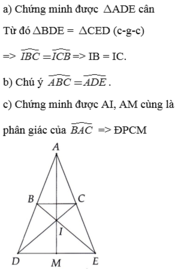
a) Xét ΔABI và ΔACI có
AB=AC(gt)
AI chung
BI=CI(I là trung điểm của BC)
Do đó: ΔABI=ΔACI(c-c-c)
b) Xét ΔAIC và ΔDIB có
IA=ID(gt)
\(\widehat{AIC}=\widehat{DIB}\)(hai góc đối đỉnh)
IC=IB(I là trung điểm của BC)
Do đó: ΔAIC=ΔDIB(c-g-c)
⇒\(\widehat{ACI}=\widehat{DBI}\)(hai góc tương ứng)(1)
mà \(\widehat{ACI}\) và \(\widehat{DBI}\) là hai góc ở vị trí so le trong
nên AC//BD(Dấu hiệu nhận biết hai đường thẳng song song)
c) Xét ΔAIB và ΔDIC có
AI=DI(gt)
\(\widehat{AIB}=\widehat{DIC}\)(hai góc đối đỉnh)
IB=IC(I là trung điểm của BC)
Do đó: ΔAIB=ΔDIC(c-g-c)
⇒AB=CD(hai cạnh tương ứng)
mà AB=AC(gt)
nên CD=AC
Xét ΔACI và ΔDCI có
CA=CD(cmt)
CI chung
IA=ID(gt)
Do đó: ΔACI=ΔDCI(c-c-c)
⇒\(\widehat{ACI}=\widehat{DCI}\)(hai góc tương ứng)
mà \(\widehat{ACI}+\widehat{DCI}=\widehat{ACD}\)(tia CI nằm giữa hai tia CA,CD)
nên \(\widehat{ACD}=2\cdot\widehat{ACI}\)(2)
Từ (1) và (2) suy ra \(\widehat{ACD}=2\cdot\widehat{DBC}\)(đpcm)

a: Xét ΔAIB và ΔAIE có
AI chung
\(\widehat{BAI}=\widehat{EAI}\)
AB=AE
Do đó: ΔAIB=ΔAIE
b: Xét ΔABD và ΔAED có
AB=AE
\(\widehat{BAD}=\widehat{EAD}\)
AD chung
Do đó: ΔABD=ΔAED
Suy ra: DB=DE
Ta có: AB=AE
nên A nằm trên đường trung trực của BE(1)
Ta có: DB=DE
nên D nằm trên đường trung trực của BE(2)
Từ (1) và (2) suy ra AD là đường trung trực của BE
hay AD\(\perp\)BE
a) Ta có: \(\widehat{ABC}+\widehat{ABD}=180^0\)
hay \(80^0+\widehat{ABD}=180^0\)
\(\widehat{ABD}=180^0-80^0\)
\(\widehat{ABD}=100^0\)
\(\Delta ABD\) có: \(\widehat{ADB}+\widehat{ABD}+\widehat{DAB}=180^0\)
hay \(30^0+100^0+\widehat{DAB}=180^0\)
\(\widehat{DAB}=180^0-\left(30^0+100^0\right)\)
\(\widehat{DAB}=50^0\)
b) Xét \(\Delta AIE\) và \(\Delta BID\), ta có:
IA=IB ( vì I là trung điiểm của AB)
\(\widehat{AIE}=\widehat{BID}\) ( đối đỉnh)
IE=ID ( gt)
\(\Rightarrow\Delta AIE=\Delta BID\) (c-g-c)
\(\Rightarrow\widehat{AEI}=\widehat{IDB}\) ( 2 góc tương ứng) mà hai góc này ở vị trí so le trong nên AE//BD (đpcm)
c) để chiều nha! (mik mệt rùi )
)