Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: XétΔABD và ΔAED có
AB=AE
\(\widehat{BAD}=\widehat{EAD}\)
AD chung
Do đó:ΔABD=ΔAED
Suy ra: BD=ED
b: ta có: BD=ED
mà ED<DC
nên BD<DC


c. Vì ΔABD = ΔAED ⇒ BD = DE (hai cạnh tương ứng)(0.5 điểm)
Vì ∠(xBC) là góc ngoài của tam giác ABC nên ∠(xBC) > ∠C (0.5 điểm)
Mà ∠(xBC) = ∠(DEC) ̂⇒ ∠(DEC) > ∠C (0.5 điểm)
Trong tam giác ΔDEC có ∠(DEC) > ∠C ⇒ DC > DE mà DE = BD (0.5 điểm)
Suy ra DC > BD (0.5 điểm)

a) Xét ∆ADE và ∆ADB ta có:
AE = AB (gt)
(AD là tia phân giác của )
AD (cạnh chung)
Do đó ∆ADE = ∆ADB (c.g.c)
Mà là góc ngoài của tam giác ADE
Nên
b) Ta có là góc ngoài của tam giác ACD)
Mà (câu a)
∆CDE có DC > ED (định lí cạnh đối diện với góc lớn hơn)
Mà ED = BD (∆ADE = ∆ADB). Do vậy DC>BD.

a) Xét ΔABD và ΔAED có
AB=AE(gt)
\(\widehat{BAD}=\widehat{EAD}\)(AD là tia phân giác của \(\widehat{BAE}\))
AD chung
Do đó: ΔABD=ΔAED(c-g-c)
Suy ra: BD=ED(hai cạnh tương ứng)


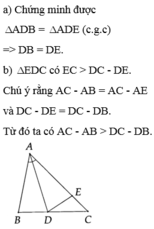
a: Xét ΔABC có AD là phân giác
nên BD/AB=CD/AC
mà AB<AC
nên BD<DC
b: Xét ΔABD và ΔAED có
AB=AE
\(\widehat{BAD}=\widehat{EAD}\)
AD chung
Do đó: ΔABD=ΔAED
Suy ra: BD=DE