
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


(a) và (b) không song song nên (a) cắt (b), gọi giao điểm là O. Tam giác OSQ có PQ và RS là hai đường cao gặp nhau tại M nên M là trực tâm của tam giác nên đường thẳng vẽ từ M và vuông góc với SQ là đường cao thứ ba của tam giác tức là đường vuông góc với SQ vẽ từ M cũng đi qua giao điểm của a và b
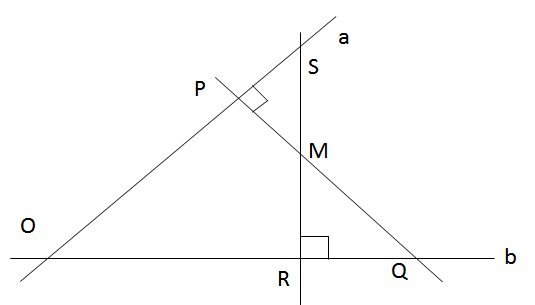
(a) và (b) không song song nên (a) cắt (b), gọi giao điểm là O. Tam giác OSQ có PQ và RS là hai đường cao gặp nhau tại M nên M là trực tâm của tam giác nên đường thẳng vẽ từ M và vuông góc với SQ là đường cao thứ ba của tam giác tức là đường vuông góc với SQ vẽ từ M cũng đi qua giao điểm của a và b

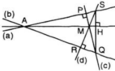
Gọi A là giao điểm của a và b.
Theo giả thiết c ⟘ a hay SR ⟘ AQ hay SR là đường cao của ΔASQ.
d ⟘ b hay PQ ⟘ AS hay QP là đường cao của ΔASQ.
SR cắt QP tại M ⇒ M là trực tâm của ΔASQ
⇒ AM ⟘ SQ
Vậy đường thẳng đi qua M và vuông góc với SQ cũng đi qua A (đpcm).

Trên mặt phẳng có đường thẳng c cắt đường thẳng a tức k song song với a
=> Đường thẳng c cũng không song song với b
Hình như dùng Ơ clit nhưng xl mình quên rồi

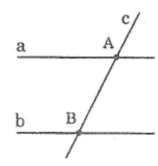
Ta có: a//b, c cắt a tại A
Giả sử c không cắt b thì suy ra c//b
Vậy qua điểm A kẻ được 2 đường thẳng a và c phân biệt cùng song song với b trái với tiên đề Ơ-clit
Vậy a//b, c cắt a thì c cắt b

Xét tam giác BCD ta có:
\(AB=AC=AD\) (gt) mà CA là trung tuyến của BD
Do đó tam giác BCD vuông tại C (do trong tam giác trung tuyến ứng vs 1 cạnh mà bằng nửa cạnh đó thì tam giác đó vuông)
\(\Rightarrow DC\perp BC\)
Vì AE và CD phân biệt mà \(AE\perp BC\left(gt\right);DC\perp BC\left(cmt\right)\)
=> AE//DC ( do hai đường thẳng phân biệt cùng vuông góc vs đường thẳng thứ 3 thì hai đường thẳng đó song song) (đpcm)
Chúc bạn học tốt!!!
giả sử c ko cắt b.
suy ra c//b. Theo tiên đề Ơ-cơ-lit, qua 1 điểm cho trước ( điểm H đóa) ta chỉ vẽ được 1 và chỉ 1 đường thẳng // với 1 đường thẳng đã cho. Ở đây vẽ dc c//a và c//b => mâu thuẫn
Vậy c cắt b b tick **** chi mik nhs