
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Lời giải:
Giả sử $(a^2+b^2, ab)>1$. Khi đó, gọi $p$ là ước nguyên tố lớn nhất của $(a^2+b^2,ab)$
$\Rightarrow a^2+b^2\vdots p; ab\vdots p$
Vì $ab\vdots p\Rightarrow a\vdots p$ hoặc $b\vdots p$
Nếu $a\vdots p$. Kết hợp $a^2+b^2\vdots p\Rightarrow b^2\vdots p$
$\Rightarrow b\vdots p$
$\Rightarrow p=ƯC(a,b)$ . Mà $(a,b)=1$ nên vô lý
Tương tự nếu $b\vdots p$
Vậy điều giả sử là sai. Tức là $(a^2+b^2, ab)=1$

Số chính phương khi chia 3 chỉ dư 0 hoặc 1.
Trường hợp 1:
\(a^2\equiv1\left(mod3\right);b^2\equiv0\left(mod3\right)\Leftrightarrow a^2+b^2\equiv1\left(mod3\right)\)(loại)
Trường hợp 2:
\(a^2\equiv1\left(mod\right)3;b^2\equiv1\left(mod3\right)\Leftrightarrow a^2+b^2\equiv2\left(mod3\right)\)(loại)
Trường hợp 3:
\(a^2\equiv0\left(mod3\right);b^2\equiv0\left(mod3\right)\Leftrightarrow a^2+b^2\equiv0\left(mod3\right)\) ( thỏa mãn )
Vậy có đpcm.
Giải:
Giả sử a không ⋮ 3 ➩ b không ⋮ 3
➩\(a^2 - 1 + b^2-1\) ⋮ 3
Mà \(a^2 +b^2\)➩2⋮ 3 (không có thể)
Vậy ➩a và b ⋮ 3.

|
Xét tổng
Suy ra có ít nhất một trong 7 số |
![]()
![]() là số chẵn
là số chẵn



a, a(b+c)−b(a−c)a(b+c)−b(a−c)
=ab+ac−(ab−bc)=ab+ac−(ab−bc)
=ab+ac−ab+bc=ab+ac−ab+bc
=ac+bc=ac+bc
=(a+b)c=(a+b)c
b,(a+b)(a−b)(a+b)(a−b)
=(aa+ab)−(ab+bb)=(aa+ab)−(ab+bb)
=aa+ab−ab−bb

Với a = -7 và b = 4. Ta có:
a2 – b2 = (-7)2 – 42 = 49 – 16 = 33
(a + b).(a –b) = [(-7) + 4].[(-7) - 4 ] = (-3).(-11) = 33

a^3+b^3+c^3-3abc
=(a+b)^3+c^3-3ab(a+b)-3bca
=(a+b+c)(a^2+2ab+b^2-ac-bc+c^2)-3ab(a+b+c)
=(a+b+c)(a^2+b^2+c^2-ab-ac-bc)

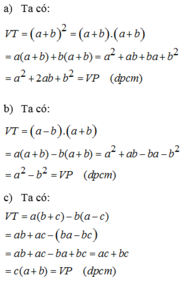
bài này hình như đăng nhiều lắm, nhìn quen quen