Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét ΔHBA vuông tại H và ΔABC vuông tại A có
góc B chung
=>ΔHBA đồng dạng với ΔABC
b: \(BC=\sqrt{6^2+8^2}=10\left(cm\right)\)
CD là phângíac
=>AD/AC=DB/CB
=>AD/3=DB/5=(AD+DB)/(3+5)=8/8=1
=>AD=3cm; BD=5cm

a: Xet ΔABC vuông tại A và ΔHBA vuôngtại H có
góc B chung
=>ΔABC đồng dạngvới ΔHBA
b: Xet ΔCHM vuông tại H và ΔCKB vuông tại K có
góc HCM chung
=>ΔCHM đồng dạngvới ΔCKB
=>CH/CK=CM/CB
=>CH*CB=CK*CM
c: Xét ΔBHD vuông tại H và ΔBKC vuông tại K có
goc HBD chung
=>ΔBHD đồng dạng với ΔBKC
=>BH/BK=BD/BC
=>BH/BD=BK/BC
=>ΔBHK đồng dạng vơi ΔBDC
=>góc BKH=góc BCD

a: Xét tứ giác ADME có
\(\widehat{ADM}=\widehat{AEM}=\widehat{DAE}=90^0\)
Do đó: ADME là hình chữ nhật
b: Xét ΔABC có
M là trung điểm của BC
ME//AB
Do đó: E là trung điểm của AC
c: Xét tứ giác AMCN có
E là trung điểm của AC
E là trung điểm của MN
Do đó: AMCN là hình bình hành
mà MA=MC
nên AMCN là hình thoi

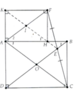
a) F H A ^ = H A K ^ = A K F ^ = 90 0
Þ AHFK là hình chữ nhật.
b) Gọi là giao điểm của AC và BD. Chứng minh OE là đường trung bình của DACF
Þ AF//OE
Þ AF/BD
c) Gọi I là giao điểm của AF và HK.
Chứng minh
H 1 ^ = A ^ 1 ( H 1 ^ = A 2 ^ = B 1 ^ = A 1 ^ ) ⇒ K H / / A C mà KH đi qua trung điểm I của AF Þ KH đi qua trung điểm của FC.
Mà E là trung điểm của FC Þ K, H, E thẳng hàng
a: Xét ΔBAC vuông tại A và ΔBMA vuông tại M có
góc B chung
=>ΔBAC đồng dạng với ΔBMA
b: Xét ΔBMH vuông tại M và ΔBKC vuông tại K có
góc MBH chung
=>ΔBMH đồng dạng với ΔBKC
=>BM/BK=BH/BC
=>BM*BC=BK*BH
c:
góc AMB=góc AIB=90 độ
=>ABMI nội tiếp
=>góc AIM=180 độ-góc ABC
góc AIK+góc ATK=90 độ+90 độ=180 độ
=>AIKT nội tiếp
=>góc AIT=góc AKT
góc BAC=góc BKC=90 độ
=>BAKC nội tiếp
=>góc ABC+góc AKC=180 độ
=>góc ABC=góc AKY=góc AIT
góc MIT=góc AIM+góc AIT
=180 độ-góc ABC+góc ABC
=180 độ
=>M,I,T thẳng hàng