B
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
LS
2
5 tháng 12 2021
b: \(=\left(\cos^2\alpha+\sin^2\alpha\right)^3-3\cos^2\alpha\sin^2\alpha\left(\sin^2\alpha+\cos^2\alpha\right)+3\cdot\sin^2\alpha\cdot\cos^2\alpha\)
=1
NV
Nguyễn Việt Lâm
Giáo viên
5 tháng 12 2021
\(cos^4a-sin^4a+1=\left(cos^2a-sin^2a\right)\left(cos^2a+sin^2a\right)+1\)
\(=cos^2a-sin^2a+1=cos^2a-sin^2a+sin^2a+cos^2a\)
\(=2cos^2a\)
\(cos^6a+sin^6a+3sin^2a.cos^2a\)
\(=\left(cos^2a+sin^2a\right)^3-3sin^2a.cos^2a\left(sin^2a+cos^2a\right)+3sin^2a.cos^2a\)
\(=1-3sin^2a.cos^2a.1+3sin^2a.cos^2a\)
\(=1\)
15 tháng 11 2023
Câu 1:
a: \(A=15\sqrt{4a}+\sqrt{a}-\sqrt{25a}\)
\(=15\cdot2\sqrt{a}+\sqrt{a}-5\sqrt{a}\)
\(=30\sqrt{a}-4\sqrt{a}=26\sqrt{a}\)
b: Sửa đề: Khi a=100
Thay a=100 vào A, ta được:
\(A=26\cdot\sqrt{100}=26\cdot10=260\)
CN
2
5 tháng 6 2020
\(sin^2a+cos^2a-sin^4a-2cos^2a+sin^2a\)
\(=2sin^2a-cos^2a-sin^4a\)
\(=2sin^2a-cos^2a-\left(\frac{1-cos2a}{2}\right)^2\)
khai triển ra rồi quy đồng lên
\(=\frac{8sin^2a-4cos^2a-1+2cos2a-cos^22a}{4}\)
Mà \(2cos2a=2\left(cos^2a-1\right)=4cos^2-2\)
\(\Rightarrow\frac{8sin^2a-cos^22a-3}{4}\)
Mà \(-cos^22a=sin^22a-1=4sin^2cos^2-1\)
\(\Rightarrow\frac{8sin^2a+4sin^2a.cos^2a-4}{4}\)
\(=\frac{4sin^2a.\left(2-cos^2a\right)-4}{4}\)
\(=sin^2a\left(1+sin^2a\right)-1\)
\(=sin^4a-cos^2a\)
VT
2
11 tháng 9 2017
A= \(\left(\sin^2a\right)^3+\left(cos^2a\right)^3+3sin^2acos^2a\)
=\(\left(sin^2a+cos^2a\right)\left(sin^4a-cos^2asin^2a+cos^4a\right)+3sin^2acos^2a\)
\(sin^4a+2sin^2acos^2a+cos^4a=\left(sin^2+cos^2\right)^2=1^2=1\)
F
20 tháng 8 2021
1.
A= \(2\sqrt{6}\) + \(6\sqrt{6}\) - \(8\sqrt{6}\)
A= 0
2.
A= \(12\sqrt{3}\) + \(5\sqrt{3}\) - \(12\sqrt{3}\)
A= 0
3.
A= \(3\sqrt{2}\) - \(10\sqrt{2}\) + \(6\sqrt{2}\)
A= -\(\sqrt{2}\)
4.
A= \(3\sqrt{2}\) + \(4\sqrt{2}\) - \(\sqrt{2}\)
A= \(6\sqrt{2}\)
5.
M= \(2\sqrt{5}\) - \(3\sqrt{5}\) + \(\sqrt{5}\)
M= 0
6.
A= 5 - \(3\sqrt{5}\) + \(3\sqrt{5}\)
A= 5
This literally took me a while, pls sub :D
https://www.youtube.com/channel/UC4U1nfBvbS9y_Uu0UjsAyqA/featured
CM
12 tháng 7 2017
x + 2 x - 3 = x - x + 3 x - 3 = x ( x - 1) + 3( x - 1) = ( x - 1)( x + 3)
a) Với điểu kiện x ≥ 0; x ≠ 1 ta có:
9 tháng 11 2017
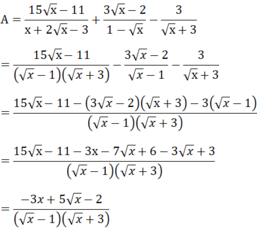
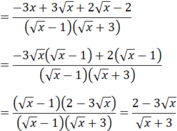
Đặt \(\sin^2\alpha=x\Rightarrow\cos^2\alpha=1-\sin^2\alpha\)
\(A=x^3+\left(1-x\right)^3+3x-\left(1-x\right)=x^3+1-3x+3x^2-x^3+3x-1+x=3x^2+x\)
Vậy \(A=3\sin^4\alpha+\sin^2\alpha\). NHỚ NHA!
18 tháng 5 2021
`a)đk:a>0,a ne 9`
`A=((sqrta+3+sqrta-3)/(a-9)).((sqrta-3)/sqrta)`
`=((2sqrtx)/(a-9)).((sqrta-3)/sqrta)`
`=2/(sqrta+3)`
`b)A>1/2`
`<=>2/(sqrta+3)>1/2`
`<=>sqrta+3<4`
`<=>sqrta<1`
`<=>a<1`
KẾt hợp đkxđ:`0<x<1`
18 tháng 5 2021
ĐKXĐ: \(\left\{{}\begin{matrix}a>0\\a\ne9\end{matrix}\right.\)
a) Ta có: \(A=\left(\dfrac{1}{\sqrt{a}-3}+\dfrac{1}{\sqrt{a}+3}\right)\left(1-\dfrac{3}{\sqrt{a}}\right)\)
\(=\dfrac{\sqrt{a}+3+\sqrt{a}-3}{\left(\sqrt{a}-3\right)\left(\sqrt{a}+3\right)}\cdot\dfrac{\sqrt{a}-3}{\sqrt{a}}\)
\(=\dfrac{2\sqrt{a}}{\sqrt{a}+3}\cdot\dfrac{1}{\sqrt{a}}\)
\(=\dfrac{2}{\sqrt{a}+3}\)
b) Để \(A>\dfrac{1}{2}\) thì \(A-\dfrac{1}{2}>0\)
\(\Leftrightarrow\dfrac{2}{\sqrt{a}+3}-\dfrac{1}{2}>0\)
\(\Leftrightarrow\dfrac{4-\left(\sqrt{a}+3\right)}{2\left(\sqrt{a}+3\right)}>0\)
mà \(2\left(\sqrt{a}+3\right)>0\forall a\)
nên \(1-\sqrt{a}>0\)
\(\Leftrightarrow\sqrt{a}< 1\)
hay a<1
Kết hợp ĐKXĐ, ta được: 0<a<1
\(A=\left(sin^2a+cos^2a\right)^3-3\cdot sin^2a\cdot cos^2a\left(sin^2a+cos^2a\right)+3\cdot sin^2a\cdot cos^2a\)
\(=1-3\cdot sin^2a\cdot cos^2a+3\cdot sin^2a\cdot cos^2a\)
=1