
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

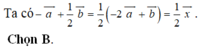

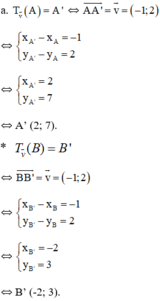
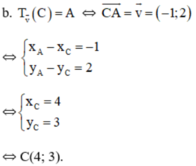
c) Đường thẳng d có vecto pháp tuyến là n→(1;-2) nên 1 vecto chỉ phương của d là(2; 1)
=> Vecto v→ không cùng phương với vecto chỉ phương của đường thẳng d
=> Qua phép tịnh tiến v→ biến đường thẳng d thành đường thẳng d’ song song với d.
Nên đường thẳng d’ có dạng : x- 2y + m= 0
Lại có B(-1; 1) d nên B’(-2;3) d’
Thay tọa độ điểm B’ vào phương trình d’ ta được:
-2 -2.3 +m =0 ⇔ m= 8
Vậy phương trình đường thẳng d’ là:x- 2y + 8 = 0

Lời giải:
Coi \(ABCD\) là mặt đáy.
Trên tia đối của tia $BA$ lấy $T$ sao cho $BT=BA$. Khi đó:
\(\overrightarrow {AB}=\overrightarrow{BT}; \overrightarrow{CT}=\overrightarrow{DB}\)
Ta có:
\(\overrightarrow{OM}=\frac{1}{2}(\overrightarrow{a}-\overrightarrow{b})\)
\(\Leftrightarrow 2\overrightarrow{OM}=\overrightarrow{AB}-\overrightarrow{BC}=\overrightarrow{BT}-\overrightarrow {BC}\)
\(\Leftrightarrow 2\overrightarrow{OM}=\overrightarrow{CT}=\overrightarrow{DB}\Leftrightarrow \overrightarrow{OM}=\frac{1}{2}\overrightarrow{DB}\)
Lấy $K$ là trung điểm của $BB'$
Vì $O$ là tâm hình hộp nên $O$ là trung điểm $B'D$
\(\Rightarrow OK\parallel BD; OK=\frac{1}{2}BD\)
\(\Rightarrow \overrightarrow{OK}=\frac{1}{2}{DB}\)
Do đó \(K\equiv M\) hay M là trung điểm của $BB'$

3 mệnh đều đầu đúng, mệnh đề thứ 4 sai
Mệnh đề 4 sai ở chỗ khi d vuông góc với 2 đường thẳng thuộc (x) song song với nhau thì d chưa chắc vuông góc (x)
Mệnh đề đúng phải là: nếu đường thẳng d vuông góc 2 đường thẳng phân biệt cắt nhau cùng thuộc một mặt phẳng (x) thì d vuông góc (x)

Trong mặt phẳng với hệ trục Oxy, ảnh của điểm M(x;y) qua phép tịnh tiến vectơ là:
A. M' (a - x; b - y)
B. M' (x + b; y + a)
C. M' (-x + a; y + b)
D. M' (x + a; y + b)
Giải thích;
\(M'\left(x';y'\right)=T_{\overrightarrow{v}}\left(M\right)\)
\(\Rightarrow\left\{{}\begin{matrix}x'-x=a\\y'-y=b\end{matrix}\right.\)\(\Rightarrow\left\{{}\begin{matrix}x'=x+a\\y'=y+b\end{matrix}\right.\)
\(\Rightarrow M'\left(x+a;y+b\right)\)
Chọn D.