Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

2 : cho ab=cd(a,b,c,d≠0)ab=cd(a,b,c,d≠0) và đôi 1 khác nhau, khác đôi nhau
Chứng minh :
a) C1: Đặt \(\frac{a}{b}=\frac{c}{d}=k\)\(\Rightarrow\left\{{}\begin{matrix}a=kb\\c=kd\end{matrix}\right.\)
\(\frac{a-b}{a+b}=\frac{kb-b}{kb+b}=\frac{b\left(k-1\right)}{b\left(k+1\right)}=\frac{k-1}{k+1}\)
\(\frac{c-d}{c+d}=\frac{kd-d}{kd+d}=\frac{d\left(k-1\right)}{d\left(k+1\right)}\frac{k-1}{k+1}\)
Bài 1:
a: Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{x}{2}=\dfrac{y}{\dfrac{3}{2}}=\dfrac{z}{\dfrac{4}{3}}=\dfrac{x-y}{2-\dfrac{3}{2}}=\dfrac{15}{\dfrac{1}{2}}=30\)
Do đó: x=60; y=45; z=40
b: Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{x}{10}=\dfrac{y}{15}=\dfrac{z}{21}=\dfrac{x+y+z}{10+15+21}=\dfrac{92}{46}=2\)
Do đó: x=20; y=30; z=42

heo me tim gtnn gtln cua bieu thuc:asinx + bcosx (a,b la hang so,a^2+b^2=/o)? | Yahoo Hỏi & Đáp

Để giá trị của giới hạn là một số thực xác định thì biểu thức trên tử số ít nhất phải có nghiệm kép \(x=1\)
Đặt \(f\left(x\right)=\sqrt{3x-2}+\sqrt[3]{3x+5}+ax+b\)
\(f\left(1\right)=a+b+3=0\Rightarrow b=-3-a\)
Thay ngược lại vào \(f\left(x\right)\)
\(f\left(x\right)=\sqrt{3x-2}+\sqrt[3]{3x+5}+ax-3-a\)
\(f\left(x\right)=\frac{3\left(x-1\right)}{\sqrt{3x-2}+1}+\frac{3\left(x-1\right)}{\sqrt[3]{\left(3x+5\right)^2}+2\sqrt[3]{3x+5}+4}+a\left(x-1\right)\)
\(f\left(x\right)=\left(x-1\right)\left(\frac{3}{\sqrt{3x-2}+1}+\frac{3}{\sqrt[3]{\left(3x+5\right)^2}+2\sqrt[3]{3x+5}+4}+a\right)\)
\(\Rightarrow\) Để \(f\left(x\right)\) có nghiệm kép \(x=1\) thì
\(g\left(x\right)=\frac{3}{\sqrt{3x-2}+1}+\frac{3}{\sqrt[3]{\left(3x+5\right)^2}+2\sqrt[3]{3x+5}+4}+a\) có ít nhất một nghiệm \(x=1\)
\(g\left(1\right)=\frac{3}{2}+\frac{3}{4+4+4}+a=0\Rightarrow a=-\frac{7}{4}\Rightarrow b=-\frac{5}{4}\)
\(\Rightarrow\lim\limits_{x\rightarrow1}\frac{\sqrt{3x-2}+\sqrt[3]{3x+5}-\frac{7}{4}x-\frac{5}{4}}{x^2-2x+1}=-\frac{37}{32}\)
\(\Rightarrow P=\frac{-\frac{7}{4}-\frac{5}{4}}{-\frac{37}{32}}=\frac{96}{37}\)
Chỉ cần viết tử số thôi nhé, ta quy đồng 4 lên rồi đưa 4 xuông mẫu, sau đó tách tử số thành
\(\frac{1}{4}\left(4\sqrt{3x-2}-2\left(3x-1\right)+4\sqrt[3]{3x+5}-\left(x+7\right)\right)\)
\(=\frac{1}{4}\left(\frac{2\left[4\left(3x-2\right)-\left(3x-1\right)^2\right]}{2\sqrt{3x-2}+3x-1}+\frac{4^3\left(3x+5\right)-\left(x+7\right)^3}{16\sqrt[3]{\left(3x+5\right)^2}+4\sqrt[3]{3x+5}\left(x+7\right)+\left(x+7\right)^2}\right)\)
\(=\frac{1}{4}\left(\frac{2\left(18x-9x^2-9\right)}{2\sqrt{3x-2}+3x-1}+\frac{45x-x^3-21x^2-23}{16\sqrt[3]{\left(3x+5\right)^2}+4\sqrt[3]{3x+5}\left(x+7\right)+\left(x+7\right)^2}\right)\)
\(=\frac{1}{4}\left(\frac{-18\left(x^2-2x+1\right)}{2\sqrt{3x-2}+3x-1}+\frac{-\left(x+23\right)\left(x^2-2x+1\right)}{16\sqrt[3]{\left(3x+5\right)^2}+4\sqrt[3]{3x+5}\left(x+7\right)+\left(x+7\right)^2}\right)\)
\(=\frac{\left(x^2-2x+1\right)}{4}\left(\frac{-18}{2\sqrt{3x-2}+3x-1}-\frac{x+23}{16\sqrt[3]{\left(3x+5\right)^2}+4\sqrt[3]{3x+5}\left(x+7\right)+\left(x+7\right)^2}\right)\)
Rút gọn \(x^2-2x+1\) với mẫu số và thay \(x=1\) vào
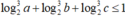 . Khi biểu thức
. Khi biểu thức 
Đáp án đúng : C