Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

ko biết mk làm có đúng ko nhma có gì sai thì đừng trách mk nhé
\(7\left(\dfrac{1}{a^2}+\dfrac{1}{b^2}+\dfrac{1}{c^2}\right)\ge\dfrac{63}{a^2+b^2+c^2}\)
\(6\left(\dfrac{1}{ab}+\dfrac{1}{bc}+\dfrac{a}{ac}\right)+2021\ge\dfrac{54}{ab+bc+ac}+2021\ge\dfrac{54}{a^2+b^2+c^2}+2021\)
<=>\(\dfrac{1}{a^2+b^2+c^2}\ge\dfrac{2021}{9}\)
\(p^2=\left(\dfrac{1}{\sqrt{3\left(2a^2+b^2\right)}}+\dfrac{1}{\sqrt{3\left(2b^2+c^2\right)}}+\dfrac{1}{\sqrt{3\left(2c^2+a^2\right)}}\right)^2\)
áp dụng bđt \(a^2+b^2+c^2\ge\dfrac{1}{3}\left(a+b+c\right)^2\)
\(p^2\le3.\left(\dfrac{1}{3\left(2a^2+b^2\right)}+\dfrac{1}{3\left(2b^2+c^2\right)}+\dfrac{1}{3\left(2c^2+a^2\right)}\right)=\dfrac{1}{2a^2+b^2}+\dfrac{1}{2b^2+c^2}+\dfrac{1}{2c^2+a^2}\)
\(< =>p^2\le\dfrac{9}{2a^2+b^2+2b^2+c^2+2c^2+a^2}\)
<=> \(p^2\le3.\dfrac{1}{a^2+b^2+c^2}=\dfrac{2021}{3}< =>p\le\sqrt{\dfrac{2021}{3}}\)
dấu bằng xảy ra khi \(a=b=c=\sqrt{\dfrac{3}{2021}}\)
\(7\left(\dfrac{1}{a^2}+\dfrac{1}{b^2}+\dfrac{1}{c^2}\right)=6\left(\dfrac{1}{ab}+\dfrac{1}{bc}+\dfrac{1}{ac}\right)+2021\le6\left(\dfrac{1}{a^2}+\dfrac{1}{b^2}+\dfrac{1}{c^2}\right)+2021\)
\(\Rightarrow2021\ge\dfrac{1}{a^2}+\dfrac{1}{b^2}+\dfrac{1}{c^2}\ge\dfrac{1}{3}\left(\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}\right)^2\)
\(\Rightarrow\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}\le\sqrt{2021.3}=\sqrt{6063}\)
Từ đó:
\(\sqrt{3\left(2a^2+b\right)}=\sqrt{\left(2+1\right)\left(2a^2+b^2\right)}\ge\sqrt{\left(2a+b\right)^2}=2a+b\)
\(\Rightarrow\dfrac{1}{\sqrt{3\left(2a^2+b^2\right)}}\le\dfrac{1}{2a+b}=\dfrac{1}{a+a+b}\le\dfrac{1}{9}\left(\dfrac{2}{a}+\dfrac{1}{b}\right)\)
Tương tự: \(\dfrac{1}{\sqrt{3\left(2b^2+c^2\right)}}\le\dfrac{1}{9}\left(\dfrac{2}{b}+\dfrac{1}{c}\right)\) ; \(\dfrac{1}{\sqrt{3\left(2c^2+a^2\right)}}\le\dfrac{1}{9}\left(\dfrac{2}{c}+\dfrac{1}{a}\right)\)
Cộng vế:
\(\Rightarrow P\le\dfrac{1}{9}\left(\dfrac{3}{a}+\dfrac{3}{b}+\dfrac{3}{c}\right)=\dfrac{1}{3}\left(\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}\right)\le\dfrac{\sqrt{6063}}{3}\)
\(P_{max}=\dfrac{\sqrt{6063}}{3}\) khi \(a=b=c=\dfrac{3}{\sqrt{6063}}\)

\(404=3\left(\dfrac{1}{a^2}+\dfrac{1}{b^2}+\dfrac{1}{c^2}\right)-2\left(\dfrac{1}{ab}+\dfrac{1}{bc}+\dfrac{1}{ca}\right)\ge\left(\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}\right)^2-\dfrac{2}{3}\left(\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}\right)^2\)
\(\Rightarrow\left(\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}\right)^2\le1212\Rightarrow\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}\le2\sqrt{303}\)
Ta có:
\(5a^2+2ab+2b^2=\left(a-b\right)^2+\left(2a+b\right)^2\ge\left(2a+b\right)^2\)
\(\Rightarrow P\le\dfrac{1}{2a+b}+\dfrac{1}{2b+c}+\dfrac{1}{2c+a}\le\dfrac{1}{9}\left(\dfrac{2}{a}+\dfrac{1}{b}+\dfrac{2}{b}+\dfrac{1}{c}+\dfrac{2}{c}+\dfrac{1}{a}\right)=\dfrac{1}{3}\left(\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}\right)\le\dfrac{2\sqrt{303}}{3}\)

\(\dfrac{1}{\left(a+b+a+c\right)^2}\le\dfrac{1}{4\left(a+b\right)\left(a+c\right)}=\dfrac{1}{4\left(a^2+ab+bc+ca\right)}\le\dfrac{1}{64}\left(\dfrac{1}{a^2}+\dfrac{1}{ab}+\dfrac{1}{bc}+\dfrac{1}{ca}\right)\)
\(\le\dfrac{1}{64}\left(\dfrac{1}{a^2}+\dfrac{1}{a^2}+\dfrac{1}{b^2}+\dfrac{1}{c^2}\right)=\dfrac{1}{64}\left(\dfrac{2}{a^2}+\dfrac{1}{b^2}+\dfrac{1}{c^2}\right)\)
Tương tự và cộng lại:
\(P\le\dfrac{1}{64}\left(\dfrac{4}{a^2}+\dfrac{4}{b^2}+\dfrac{4}{c^2}\right)=\dfrac{1}{16}.3=\dfrac{3}{16}\)
Dấu "=" xảy ra khi \(a=b=c=1\)
Áp dụng bđt: \(\dfrac{1}{x+y}\le\dfrac{1}{4}\left(\dfrac{1}{x}+\dfrac{1}{y}\right)\left(1\right)\)
\(\dfrac{1}{2a+b+c}=\dfrac{1}{\left(a+b\right)+\left(a+c\right)}\le\dfrac{1}{4}\left(\dfrac{1}{a+b}+\dfrac{1}{a+c}\right)\)
\(\Rightarrow P\le\dfrac{1}{16}\left[\left(\dfrac{1}{a+b}+\dfrac{1}{a+c}\right)^2+\left(\dfrac{1}{a+b}+\dfrac{1}{b+c}\right)^2+\left(\dfrac{1}{b+c}+\dfrac{1}{a+c}\right)^2\right]\)\(\Rightarrow16P\le\dfrac{2}{\left(a+b\right)^2}+\dfrac{2}{\left(b+c\right)^2}+\dfrac{2}{\left(a+c\right)^2}+\dfrac{2}{\left(a+b\right)\left(b+c\right)}+\dfrac{2}{\left(a+b\right)\left(b+c\right)}+\dfrac{2}{\left(b+c\right)\left(c+a\right)}\)
Áp dụng: \(x^2+y^2+z^2\ge xy+yz+xz\left(2\right)\) với a+b=x,b+c=y,c+a=z
\(\Rightarrow16P\le\dfrac{4}{\left(a+b\right)^2}+\dfrac{4}{\left(b+c\right)^2}+\dfrac{4}{\left(c+a\right)^2}\)
Ta có: \(\dfrac{1}{\left(a+b\right)^2}\le4.16.\left(\dfrac{1}{a}+\dfrac{1}{b}\right)^2\)(do (1))
\(\Rightarrow16P\le\dfrac{1}{4}.16\left[\left(\dfrac{1}{a}+\dfrac{1}{b}\right)^2+\left(\dfrac{1}{b}+\dfrac{1}{c}\right)^2+\left(\dfrac{1}{c}+\dfrac{1}{a}\right)^2\right]=\dfrac{1}{4}\left(\dfrac{1}{a^2}+\dfrac{1}{b^2}+\dfrac{1}{c^2}+\dfrac{2}{ab}+\dfrac{2}{bc}+\dfrac{2}{ca}\right)\le\dfrac{1}{4}.4.\left(\dfrac{1}{a^2}+\dfrac{1}{b^2}+\dfrac{1}{c^2}\right)=3\)(do(2) và \(\dfrac{1}{a^2}+\dfrac{1}{b^2}+\dfrac{1}{c^2}=3\))
\(\Rightarrow P\le\dfrac{3}{16}\)
\(ĐTXR\Leftrightarrow a=b=c=1\)

Từ \(7\left(\dfrac{1}{a^2}+\dfrac{1}{b^2}+\dfrac{1}{c^2}\right)=6\left(\dfrac{1}{ab}+\dfrac{1}{bc}+\dfrac{1}{ca}\right)+2017\)
\(\Leftrightarrow7\left(\dfrac{1}{a^2}+\dfrac{1}{b^2}+\dfrac{1}{c^2}\right)\le6\left(\dfrac{1}{a^2}+\dfrac{1}{b^2}+\dfrac{1}{c^2}\right)+2017\)\(\Leftrightarrow\dfrac{1}{a^2}+\dfrac{1}{b^2}+\dfrac{1}{c^2}\le2017\)
Áp dụng BĐT Cauchy-Schwarz ta có:
\(T=\dfrac{1}{\sqrt{3\left(2a^2+b^2\right)}}+\dfrac{1}{\sqrt{3\left(2b^2+c^2\right)}}+\dfrac{1}{\sqrt{3\left(2c^2+a^2\right)}}\)
\(=\dfrac{1}{\sqrt{\left(2+1\right)\left(2a^2+b^2\right)}}+\dfrac{1}{\sqrt{\left(2+1\right)\left(2b^2+c^2\right)}}+\dfrac{1}{\sqrt{\left(2+1\right)\left(2c^2+a^2\right)}}\)
\(\le\dfrac{1}{2a+b}+\dfrac{1}{2b+c}+\dfrac{1}{2c+a}\le\dfrac{1}{9}\left(\dfrac{2^2}{2a}+\dfrac{1^2}{b}\right)+\dfrac{1}{9}\left(\dfrac{2^2}{2b}+\dfrac{1^2}{c}\right)+\dfrac{1}{9}\left(\dfrac{2^2}{2c}+\dfrac{1^2}{a}\right)\)
\(\le\dfrac{1}{9}\left(\dfrac{3}{a}+\dfrac{3}{b}+\dfrac{3}{c}\right)\)\(=\dfrac{1}{3a}+\dfrac{1}{3b}+\dfrac{1}{3c}\le\sqrt{\left(\dfrac{1}{81}+\dfrac{1}{81}+\dfrac{1}{81}\right)\left(\dfrac{9}{a^2}+\dfrac{9}{b^2}+\dfrac{9}{c^2}\right)}\)
\(\le\sqrt{\dfrac{1}{81}\cdot3\cdot9\cdot2017}=\sqrt{\dfrac{2017}{3}}\)
Vậy \(T_{Max}=\sqrt{\dfrac{2017}{3}}\) khi \(a=b=c=\sqrt{\dfrac{3}{2017}}\)
So kimochiii~

\(Q=\sum\dfrac{\left(a+b\right)^2}{\sqrt{2\left(b+c\right)^2+bc}}\ge\sum\dfrac{\left(a+b\right)^2}{\sqrt{2\left(b+c\right)^2+\dfrac{1}{4}\left(b+c\right)^2}}=\dfrac{2}{3}\sum\dfrac{\left(a+b\right)^2}{b+c}\)
\(Q\ge\dfrac{2}{3}.\dfrac{\left(a+b+b+c+c+a\right)^2}{a+b+b+c+c+a}=\dfrac{4}{3}\left(a+b+c\right)=\dfrac{4}{3}\)

\(abc\ge\left(a+b-c\right)\left(b+c-a\right)\left(c+a-b\right)\)
\(\Leftrightarrow abc\ge\left(3-2a\right)\left(3-2b\right)\left(3-2c\right)\)
\(\Leftrightarrow9abc\ge12\left(ab+bc+ca\right)-27\)
\(\Rightarrow abc\ge\dfrac{4}{3}\left(ab+bc+ca\right)-3\)
\(P\ge\dfrac{9}{a\left(b^2+bc+c^2\right)+b\left(c^2+ca+a^2\right)+c\left(a^2+ab+b^2\right)}+\dfrac{abc}{ab+bc+ca}=\dfrac{9}{\left(ab+bc+ca\right)\left(a+b+c\right)}+\dfrac{abc}{ab+bc+ca}\)
\(\Rightarrow P\ge\dfrac{3}{ab+bc+ca}+\dfrac{abc}{ab+bc+ca}=\dfrac{3+abc}{ab+bc+ca}\)
\(\Rightarrow P\ge\dfrac{3+\dfrac{4}{3}\left(ab+bc+ca\right)-3}{ab+bc+ca}=\dfrac{4}{3}\)
Dấu "=" xảy ra khi \(a=b=c=1\)

Bunhiacopxki:
\(\left(b+a+a\right)\left(b+c+\dfrac{c^2}{a}\right)\ge\left(b+\sqrt{ca}+c\right)^2\)
\(\Rightarrow\dfrac{2a^2+ab}{\left(b+\sqrt{ca}+c\right)^2}\ge\dfrac{2a^2+ab}{\left(2a+b\right)\left(b+c+\dfrac{c^2}{a}\right)}=\dfrac{a^2}{c^2+ab+bc}\)
Tương tự:
\(\dfrac{2b^2+bc}{\left(c+\sqrt{ca}+a\right)^2}\ge\dfrac{b^2}{a^2+ab+bc}\)
\(\dfrac{2c^2+ca}{\left(a+\sqrt{bc}+b\right)^2}\ge\dfrac{c^2}{b^2+ac+bc}\)
\(\Rightarrow P\ge\dfrac{a^2}{c^2+ab+ac}+\dfrac{b^2}{a^2+ab+bc}+\dfrac{c^2}{b^2+ac+bc}\)
\(\Rightarrow P\ge\dfrac{\left(a+b+c\right)^2}{a^2+b^2+c^2+2ab+2bc+2ca}=1\)
Dấu "=" xảy ra khi \(a=b=c\)

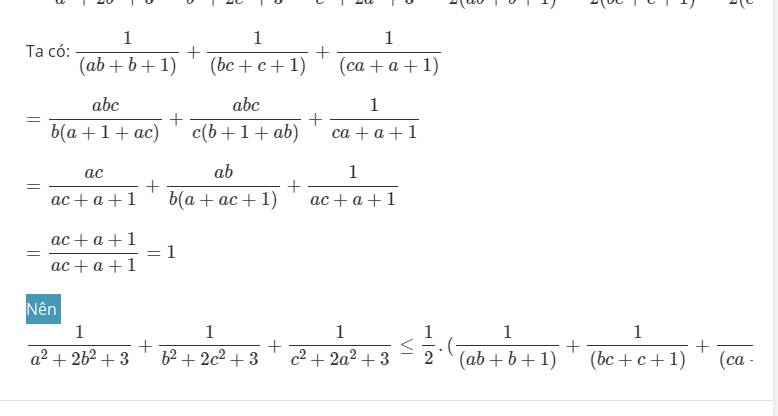

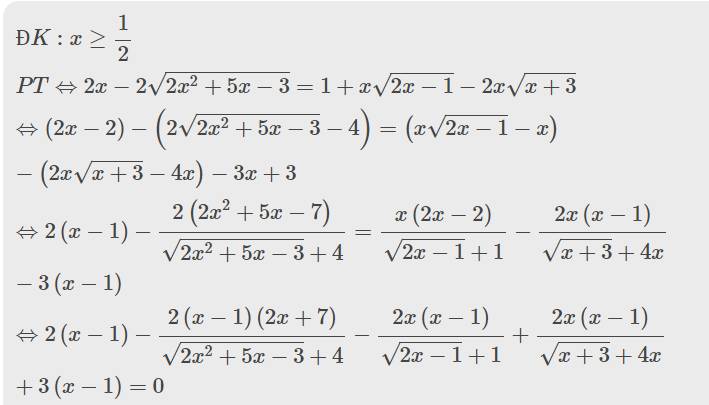

bai nay t lam roi vao trang chu cua nick thangbnsh cua t keo xuong tim la thay
Câu hỏi của Tuyển Trần Thị - Toán lớp 9 | Học trực tuyến