Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án B
3 a = 5 b = 1 3 c 5 c ⇔ a log 3 15 = b log 3 15 = - c log 15 15 ⇔ a 1 + log 3 5 = b 1 + log 5 3 = - c
Đặt t = log 3 5 ⇒ a = - c 1 + t b = - c 1 + 1 t = a t ⇒ a = - c 1 + a b ⇔ a b + b c + c a = 0
⇒ P = a + b + c 2 - 4 a + b + c ≥ - 4 . Dấu bằng khi a + b + c = 2 a b + b c + c a = 0 , chẳng hạn a = 2,b = c = 0.

Gọi M a ; b ; N c ; d
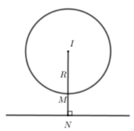
Khi đó ta có M thuộc đường tròn x - 1 2 + y - 2 2 = 1 C và N thuộc đường thẳng
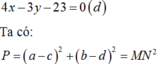
Đường tròn (C) có tâm I 1 ; 2 , bán kính R = 1
Ta có

Khi đó

Chọn D.

Đáp án D
Phương pháp:
- Phương trình đoạn chắn của mặt phẳng đi qua 3 điểm
A(a;0;0), B(0;b;0), C(0;0;c). (a, b,c khác 0): x a + y b + z c = 1
- Sử dụng bất đẳng thức: 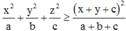
![]()
Đẳng thức xảy ra khi và chỉ khi x a = y b = z c
Cách giải:
A(a;0;0), B(0;b;0), C(0;0;c). (a, b,c > 0)
Mặt phẳng (ABC) có phương trình: x a + y b + z c = 1
Khoảng cách từ O đến (ABC):
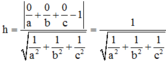
Ta có: 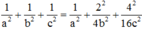
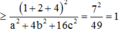
Dấu “=” xảy ra khi và chỉ khi:
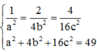
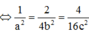
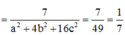
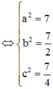
=> 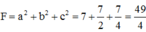
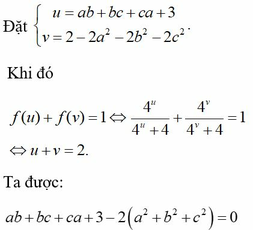
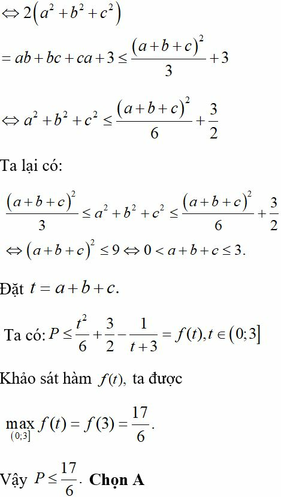



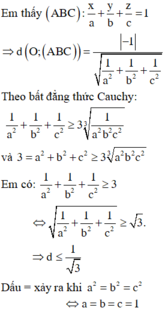

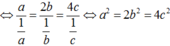
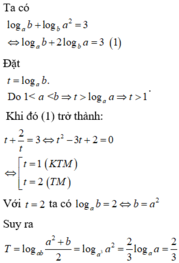
Lời giải:
Từ điều kiện đề bài dễ dàng suy ra \(a,b,c<\sqrt{3}<2\)
Sử dụng phương pháp hệ số bất định, ta sẽ CM: \(2a+\frac{1}{a}\geq \frac{5}{2}+\frac{a^2}{2}\)
BĐT này luôn đúng vì \(\Leftrightarrow (2-a)(a-1)^2\geq 0\)
Thiết lập tương tự với $b,c$, suy ra \(2(a+b+c)+\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\geq \frac{15}{2}+\frac{a^2+b^2+c^2}{2}=9\) (đpcm)
Dấu $=$ xảy ra khi $a=b=c=1$