Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(\widehat{aAb}=\widehat{a'Ab'};\widehat{bAc}=\widehat{b'Ac'};\widehat{cAa'}=\widehat{c'Aa};\widehat{aAc}=\widehat{a'Ac'};\widehat{a'Ab}=\widehat{aAb'};\widehat{cAb'}=\widehat{c'Ab}\)

a) Liệt kê các cặp góc đối đỉnh
Xét các cặp góc “đơn”:
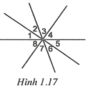
Góc 1 đối đỉnh với góc 5; Góc 2 đối đỉnh với góc 6; Góc 3 đối đỉnh với góc 7; Góc 4 đối đỉnh với góc 8. Có tất cả 4 góc “đơn” đối đỉnh.
Xét các cặp góc “ghép đôi” (ghép hai góc đơn kề nhau thành một góc “ghép đôi”):
Góc 12 đối đỉnh với góc 56; Góc 23 đối đỉnh với góc 67; Góc 34 đối đỉnh với góc 78; Góc 45 đối đỉnh với góc 81. Có tất cả 4 cặp góc “ghép đôi” đối đỉnh.
Xét các cặp góc “ghép ba” (ghép ba góc đơn kề nhau thành một góc “ghép ba”):
Góc 123 đối đỉnh với góc 567; Góc 234 đối đỉnh với góc 678; Góc 345 đối đỉnh với góc 781; Góc 456 đối đỉnh với góc 812. Có tất cả 4 cặp góc “ghép ba” đối đỉnh.
Vậy tổng cộng có 4.3 = 12 cặp góc đối đỉnh.
b) Xây dựng công thức tính số cặp góc đối đỉnh.
Có 4 đường thẳng cắt nhau tại một điểm nên có: 4.2 = 8 (tia).
Số góc do 8 tia tạo ra là 8.7 2 = 28 (góc).
Không kể góc bẹt thì số góc còn lại là: 28 − 4 = 24 (góc).
Mỗi góc trong 24 góc này đều có một góc đối đỉnh với nó nên số cặp góc đối đỉnh được tạo thành là 24 : 2 = 12 (cặp).
* Nhận xét: Nếu có n đường thẳng cắt nhau tại một điểm thì số cặp góc đối đỉnh (không kể góc bẹt) được tạo thành là n(n-1).
Thật vậy, số tia do n đường thẳng cắt nhau tại một điểm tạo ra là 2n (tia).
Số góc do 2n tia tạo ra là: 2 n 2 n − 1 2 = n 2 n − 1 .
Không kể n góc bẹt thì số góc còn lại là: n 2 n − 1 − n = 2 n 2 − n − n = 2 n 2 − 2 n = 2 n n − 1 .
Số cặp góc đối đỉnh là: 2 n n − 1 2 = n n − 1 .

a) Ta có: n n − 1 = 20 b) Ta có: n n − 1 = 90
n n − 1 = 5.4 ⇒ n = 5 . n n − 1 = 10.9 ⇒ n = 10
Vậy n = 5 . Vậy n = 10 .