Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Không gian mẫu: \(C_5^3=10\)
Chọn 3 bạn có ít nhất 2 nữ: ta có 2 trường hợp thuận lợi là 2 nữ 1 nam và 3 bạn đều nữ
\(\Rightarrow C_2^1.C_3^2+C_3^3=7\) cách
Xác suất: \(P=\dfrac{7}{10}\)
.
.
.
.
Đáp án B.
+ Rút ra 4 câu bất kì 
Có 
cách.
+ Rút ra 4 câu mà không có câu nào học thuộc 
Có 
cách.
Xác suất để bạn đó rút được 4 câu trong đó có ít nhất một câu đã học là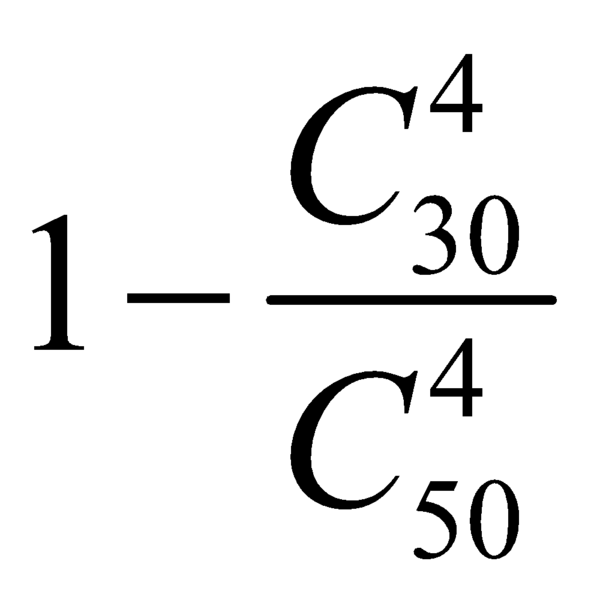 
Chọn A
Vì mỗi câu có 4 phương án trả lời và chỉ có một phương án đúng nên xác suất để chọn đúng đáp án là 1 4 , xác suất để trả lời sai là 3 4
Gọi là biến cố bạn Nam được trên 8,5 điểm thì A ¯ là biến cố bạn Nam được dưới 8,5 điểm
Vì bạn Nam đã làm chắc chắn đúng 40c âu nên để có A ¯ xảy ra 2 trường hợp
TH1: Bạn Nam chọn được một câu đúng trong 10 câu còn lại, xác suất xảy ra là:
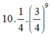
TH2: Bạn Nam chọn được hai câu đúng trong 10 câu còn lại, xác suất xảy ra là:
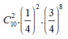
Vậy 
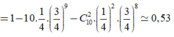
Gọi X là biến cố " chia 20 bạn thành 4 nhóm A, B, C, D mỗi nhóm 5 bạn sao cho 5 bạn nữ thuộc cùng 1 nhóm"
Ta có \(\left|\Omega\right|=C^5_{20}C^5_{10}C^5_5\) cách chia các bạn nam vào 3 nhóm còn lại.
Do vai trò các nhóm như nhau, có \(4C^5_{20}C^5_{10}C^5_5\) cách chia các bạn vào các nhóm A, B, C,D trong đó 5 bạn nữ thuộc một nhóm
Xác suất cần tìm là \(P\left(X\right)=\frac{4}{C^5_{20}}=\frac{1}{3876}\)
Lời giải:
TH1: Chọn 2 bạn lớp A, 1 bạn B, 1 bạn C, có:
$C^2_4.C^1_5.C^1_6=180$ cách chọn
TH2: Chọn 1 bạn A, 2 bạn B, 1 bạn C, có:
$C^1_4.C^2_5.C^1_6=240$ cách chọn
TH3: Chọn 1 bạn A, 1 bạn B, 1 bạn C, có:
$C^1_4.C^1_5.C^2_6=300$ cách chọn
Tổng số cách chọn: $720$ cách chọn.
1.
Không gian mẫu: \(8!\)
Xếp Quân Lâm cạnh nhau: \(2!\) cách
Coi cặp Quân-Lâm như 1 bạn, hoán vị với 6 bạn còn lại: \(7!\) cách
\(\Rightarrow2!.7!\) cách xếp thỏa mãn
Xác suất: \(P=\dfrac{2!.7!}{8!}=\dfrac{1}{4}\)
2.
Không gian mẫu: \(C_{12}^3\)
Lấy 3 bóng sao cho ko có bóng tốt nào (cả 3 đều là bóng ko tốt): \(C_4^3\) cách
\(\Rightarrow C_{12}^3-C_4^3\) cách lấy 3 bóng sao cho có ít nhất 1 bóng tốt
Xác suất: \(P=\dfrac{C_{12}^3-C_4^3}{C_{12}^3}=...\)
3.
Số tam giác bằng với số cách chọn 3 điểm từ 4 điểm nên có: \(C_4^3=...\) tam giác
4.
\(T_{\overrightarrow{v}}\left(E\right)=F\left(x;y\right)\Rightarrow\left\{{}\begin{matrix}x=-3+1=-2\\y=5-2=3\end{matrix}\right.\) \(\Rightarrow\left(-2;3\right)\)
5.
Có 2 cạnh chéo nhau với AB là SC, SD