Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: \(A\cap B=\left[2;3\right]\)
\(A\cup B=\left(-\infty;+\infty\right)\)
b: \(\left(A\cup B\right)\cap C=\left(0;4\right)\)

a.
\(A\cap B\cap C=\left[0;5\right]\)
Ý thứ 2 ko hiểu đề yêu cầu gì
b.
\(P\cap Q\ne\varnothing\Leftrightarrow\left\{{}\begin{matrix}m< 5\\m+4>-2\end{matrix}\right.\) \(\Rightarrow-6< m< 5\)

\(A=\left(-\infty;0\right);B=\left(1;+\infty\right);C=\left(0;1\right)\\ \left(A\cup B\right)\cap C=\left(-\infty;+\infty\right)\cap C=\left(0;1\right)\)


Để B tồn tại \(\Leftrightarrow2m< 3m+1\Leftrightarrow m>-1\)
TH1: \(10\le3m+1\) \(\Leftrightarrow m\ge3\)
\(A\cap B=[2m;10)\) có đúng ba số nguyên khi \(6< 2m\le7\) \(\Leftrightarrow3< m\le\dfrac{7}{2}\) ( tm đk )
TH2: \(3m+1< 10\) \(\Leftrightarrow m< 3\)
\(A\cap B=\left[2m;3m+1\right]\) có đúng ba số nguyên khi
Trường hợp m nguyên thì \(2m+2=3m+1\Leftrightarrow m=1\) (thỏa mãn)
Trường hợp m là số thực thì rộng lắm...

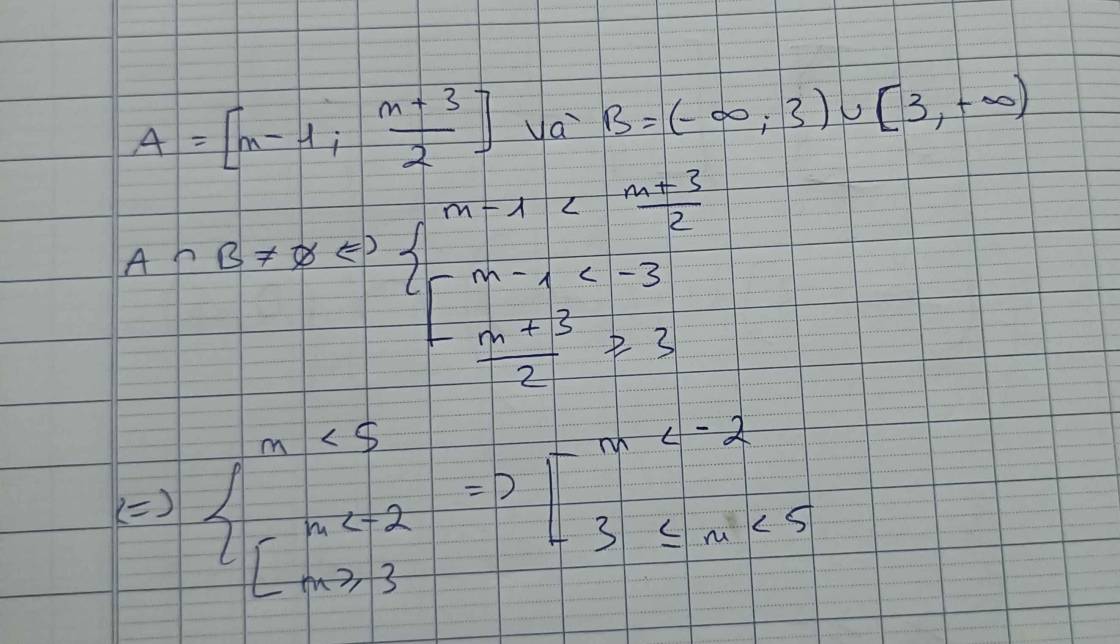
A giao B là (-2;-3)
A hợp B là (âm vô cực; 5]