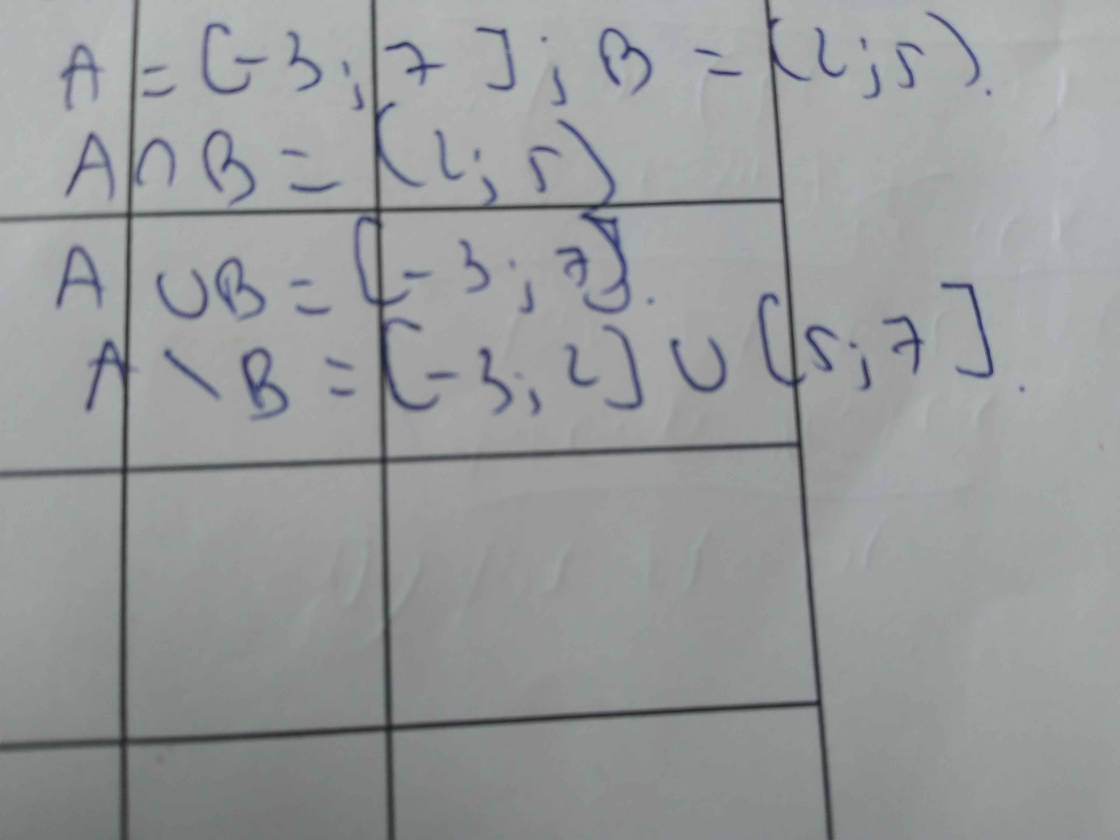
Cho 2 tập hợp: A = [ -3; 7 ]; B = ( 2; 5 ).
Xác định các tập hợp sau: \(A\cap B\); \(A\cup B\); A \ B

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Cho 2 tập hợp: A = [ -3; 7 ]; B = ( 2; 5 ).
Xác định các tập hợp sau: \(A\cap B\); \(A\cup B\); A \ B



\(A = \left\{ {0;1;2;3;4;5;6} \right\}\)
\(\,B = \left\{ {1;2;3;6;7;8} \right\}\)
Vậy
\(A \cap B = \left\{ {1;2;3;6} \right\}\)
\(A \cup B = \left\{ {0;1;2;3;4;5;6;7;8} \right\} = \left\{ {x \in \mathbb{N}|\;x < 9} \right\}\)
\(A\;{\rm{\backslash }}\;B = \left\{ {0;4;5} \right\}\)

\(E = \{ x \in \mathbb{N}|x < 8\} = \{ 0;1;2;3;4;5;6;7\} \)
a) Ta có: \(A\backslash B = \left\{ {0;1;2} \right\}\), \(B\backslash A = \left\{ 5 \right\},\)\((A\backslash B) \cap {\rm{(}}B\backslash A) = \emptyset \)
b) Ta có: \(A \cap B = \{ 3;4\} ,\;{C_E}(A \cap B) = \{ 0;1;2;5;6;7\} \)
\({C_E}A = \{ 5;6;7\} ,\;{C_E}B = \{ 0;1;2;6;7\} \Rightarrow ({C_E}A) \cap ({C_E}B) = \{ 6;7\} \)
c) Ta có: \(A \cup B = \{ 0;1;2;3;4;5\} ,\;{C_E}(A \cup B) = \{ 6;7\} \)
\({C_E}A = \{ 5;6;7\} ,\;{C_E}B = \{ 0;1;2;6;7\} \Rightarrow ({C_E}A) \cup ({C_E}B) = \{ 0;1;2;5;6;7\} \)

a) A = {đỏ; cam; vàng; lục; lam}, B = {lục; lam; chàm; tím}.
\(A \cup B = \){đỏ; cam; vàng; lục; lam; chàm; tím}
\(A \cap B = \){lục; lam}
b) Vì mỗi tam giác đều cũng là một tam giác cân nên \(A \subset B.\)
\(A \cup B = B,\;A \cap B = A.\)
Chú ý
Nếu \(A \subset B\) thì \(A \cup B = B,\;A \cap B = A.\)

a) \(\left(A\cap B\right)\cup A=A\)
b) \(\left(A\cup B\right)\cap B=B\)
c) (\(A\)\ \(B\)) \(\cup B=A\cup B\)
d) (\(A\)\ \(B\)) \(\cap\)(\(B\)\\(A\)) \(=\varnothing\)

Tham khảo:
+) \(A \cap B = [0;3] \cap (2; + \infty ) = (2;3]\)

+) \(A \cup B = [0;3] \cup (2; + \infty ) = [0; + \infty )\)

+) \(A\,{\rm{\backslash }}\,B = [0;3]\,{\rm{\backslash }}\,(2; + \infty ) = [0;2]\)

+) \(B\,{\rm{\backslash }}\,A = (2; + \infty )\,{\rm{\backslash }}\,[0;3] = (3; + \infty )\)

+) \(\mathbb{R}\,{\rm{\backslash }}\,B = \mathbb{R}\,{\rm{\backslash }}\,(2; + \infty ) = ( - \infty ;2]\)
