Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Để hai đường thẳng song song thì \(\left\{{}\begin{matrix}m-1=1-2m\\n-2\ne n+3\end{matrix}\right.\Leftrightarrow3m=2\Leftrightarrow m=\dfrac{2}{3}\)
b: Để hai đường thẳng cắt nhau thì \(m-1\ne-2m+1\)
\(\Leftrightarrow3m\ne2\)
hay \(m\ne\dfrac{2}{3}\)

a: Để hai đồ thị song song thì \(\left\{{}\begin{matrix}m^2-1=3\\m-3\ne2m-1\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m^2=4\\-m\ne2\end{matrix}\right.\Leftrightarrow m=2\)
b: Để hai đồ thị trùng nhau thì \(\left\{{}\begin{matrix}m^2-1=3\\m-3=2m-1\end{matrix}\right.\)
hay m=-2

a: Đặt (d1): \(y=\left(2m-1\right)x+n+1\)
(d2): \(y=\left(5-m\right)x-1-n\)
Để (d1) cắt (d2) thì \(2m-1\ne5-m\)
=>\(3m\ne6\)
=>\(m\ne2\)
b: Để (d1)//(d2) thì \(\left\{{}\begin{matrix}2m-1=5-m\\n+1\ne-1-n\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}3m=6\\2n\ne-2\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}m=2\\n\ne-1\end{matrix}\right.\)
c: Để \(\left(d1\right)\equiv\left(d2\right)\) thì \(\left\{{}\begin{matrix}2m-1=5-m\\n+1=-n-1\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}3m=6\\2n=-2\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}m=2\\n=-1\end{matrix}\right.\)

\(1,\Leftrightarrow m=2m+1\Leftrightarrow m=-1\\ 2,\Leftrightarrow a=-5\)

Hàm số y = mx + 3 có các hệ số a = m, b = 3.
Hàm số y = (2m + 1)x – 5 có các hệ số a' = 2m + 1, b' = -5
a) Vì hai hàm số là hai hàm số bậc nhất nên a và a' phải khác 0, tức là:
m ≠ 0 và 2m + 1 ≠ 0 hay
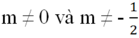
Theo đề bài ta có b ≠ b' (vì 3 ≠ -5)
Vậy đồ thị của hai hàm số là hai đường thẳng song song với nhau khi và chỉ khi a ≠ a' tức là:
m = 2m + 1 => m = - 1
Kết hợp với điều kiện trên ta thấy m = -1 là giá trị cần tìm.
b) Đồ thị của hai hàm số y = mx + 3 và y = (2m + 1)x – 5 là hai đường thẳng cắt nhau khi và chỉ khi:
m ≠ 2m + 1 => m ≠ -1.
Kết hợp với điều kiện trên, ta có:
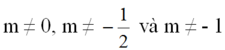

2 hàm số bậc nhất \(y=mx+3,y=\left(2m+1\right)x-5\left(đk:m\ne0,m\ne-\dfrac{1}{2}\right)\)
a) Để 2 đường thẳng song song với nhau thì:
\(\left\{{}\begin{matrix}m\ne0\\m\ne-\dfrac{1}{2}\\m=2m+1\\3\ne-5\left(luôn.đúng\right)\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}m\ne0\\m\ne-\dfrac{1}{2}\\m=-1\end{matrix}\right.\)
b) Để 2 đường thẳng cắt nhau:
\(\left\{{}\begin{matrix}m\ne0\\m\ne-\dfrac{1}{2}\\m\ne2m+1\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}m\ne0\\m\ne-\dfrac{1}{2}\\m\ne-1\end{matrix}\right.\)
c) Để 2 đường thẳng vuông góc với nhau:
\(\left\{{}\begin{matrix}m\ne0\\m\ne-\dfrac{1}{2}\\m\left(2m+1\right)=-1\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}m\ne0\\m\ne-\dfrac{1}{2}\\2m^2+m+1=0\left(VLý.do.2m^2+m+1=2\left(m+\dfrac{1}{4}\right)^2+\dfrac{7}{8}>0\right)\end{matrix}\right.\)
Vậy 2 đường thẳng này không vuông góc với nhau với mọi m
\(a,\Leftrightarrow\left\{{}\begin{matrix}m=2m+1\\-5\ne3\end{matrix}\right.\Leftrightarrow m=-1\\ b,\Leftrightarrow m\ne2m+1\Leftrightarrow m\ne-1\\ c,\Leftrightarrow m\left(2m+1\right)=-1\\ \Leftrightarrow2m^2+m+1=0\\ \Delta=1-8< 0\\ \Leftrightarrow m\in\varnothing\)
Vậy 2 đt không thể vuông góc nhau

Hàm số y = mx + 3 có các hệ số a = m, b = 3.
Hàm số y = (2m + 1)x – 5 có các hệ số a' = 2m + 1, b' = -5
Vì hai hàm số là hai hàm số bậc nhất nên a và a' phải khác 0, tức là:
m ≠ 0 và 2m + 1 ≠ 0 hay
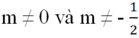
Theo đề bài ta có b ≠ b' (vì 3 ≠ -5)
Vậy đồ thị của hai hàm số là hai đường thẳng song song với nhau khi và chỉ khi a ≠ a' tức là:
m = 2m + 1 => m = - 1
Kết hợp với điều kiện trên ta thấy m = -1 là giá trị cần tìm.

Bài 1
ĐKXĐ: m ≠ 0 và m ≠ -1/2
a) Để hai đường thẳng cắt nhau thì:
3m ≠ 2m + 1
⇔ m ≠ 1
Vậy m ≠ 0; m ≠ -1/2 và m ≠ 1 thì hai đường thẳng đã cho cắt nhau
b) Để hai đường thẳng song song thì:
3m = 2m + 1
⇔ m = 1 (nhận)
Vậy m = 1 thì hai đường thẳng đã cho song song
Bài 2
ĐKXĐ: m ≠ 0 và m ≠ -1/2
a) Để hai đường thẳng đã cho cắt nhau thì:
3m ≠ 2m + 1
⇔ m ≠ 1
Vậy m ≠ 0; m ≠ -1/2; m ≠ 1 thì hai đường thẳng đã cho cắt nhau
b) Để hai đường thẳng trùng nhau thì:
3m = 2m + 1 và 4 - m² = 3
*) 3m = 2m + 1
⇔ m = 1 (nhận) (*)
*) 4 - m² = 3
⇔ m² = 4 - 3
⇔ m² = 1
⇔ m = 1 (nhận) hoặc m = -1 (nhận) (**)
Từ (*) và (**) ⇒ m = 1 thì hai đường thẳng đã cho trùng nhau
c) Để hai đường thẳng đã cho song song thì:
3m = 2m + 1 và 4 - m² ≠ 3
*) 3m = 2m + 1
⇔ m = 1 (nhận) (1)
*) 4 - m² ≠ 3
⇔ m² ≠ 1
⇔ m ≠ 1 (nhận) và m ≠ -1 (nhận) (2)
Từ (1) và (2) ⇒ Không tìm được m để hai đường thẳng đã cho song song
d) Để hai đường thẳng vuông góc thì:
3m.(2m + 1) = -1
⇔ 6m² + 3m + 1 = 0 (3)
Ta có:
6m² + 3m + 1 = 6.(m² + m/2 + 1/6)
= 6.(m² + 2.m.1/4 + 1/16 + 5/48)
= 6(m + 1/4)² + 5/8 > 0 (với mọi m)
⇒ (3) là vô lý
Vậy không tìm được m để hai đường thẳng đã cho vuông góc

Hàm số y = mx + 3 có các hệ số a = m, b = 3.
Hàm số y = (2m + 1)x – 5 có các hệ số a' = 2m + 1, b' = -5
Vì hai hàm số là hai hàm số bậc nhất nên a và a' phải khác 0, tức là:
m ≠ 0 và 2m + 1 ≠ 0 hay
Theo đề bài ta có b ≠ b' (vì 3 ≠ -5)
Vậy đồ thị của hai hàm số là hai đường thẳng song song với nhau khi và chỉ khi a ≠ a' tức là:
m = 2m + 1 => m = - 1
Kết hợp với điều kiện trên ta thấy m = -1 là giá trị cần tìm.
a: Để hai đồ thị song song thì \(\left\{{}\begin{matrix}2m-3=m\\n-2\ne3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m=3\\n\ne5\end{matrix}\right.\)
b: Để hai đồ thị cắt nhau thì \(2m-3\ne m\)
hay \(m\ne3\)