Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có :
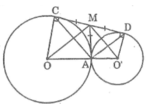
MO là tia phân giác của góc (CMA) (tính chất hai tiếp tuyến cắt nhau)
MO’ là tia phân giác của góc (DMA) (tính chất hai tiếp tuyến cắt nhau)
Suy ra : MO ⊥ MO’ (tính chất hai góc kề bù)
Tam giác MOO’ vuông tại M có MA ⊥ OO’ (tính chất tiếp tuyến)
Theo hệ thức lượng trong tam giác vuông, ta có :
M A 2 = OA.O’A = 4,5.2 = 9 ⇒ MA = 3 (cm)
Mà MA = 12 CD ⇒ CD = 2.MA = 2.3 = 6 (cm)

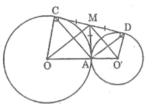
Kẻ tiếp tuyến chung tạ IA cắt CD tại M
Trong đường tròn (O) ta có:
MA = MC (tính chất hai tiếp tuyến cắt nhau)
Trong đường tròn (O’) ta có :
MA = MD (tính chất hai tiếp tuyến cắt nhau)
Suy ra : MA = MC = MD = 12 CD
Tam giác ACD có đường trung tuyến AM ứng với cạnh CD bằng nửa cạnh CD nên tam giác ACD vuông tại A
Suy ra : ![]()

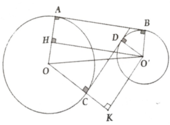
Kẻ O’H ⊥ OA; O’K ⊥ OC
OH = 4; OK = 8
Đặt CD = x => AB = 2x
O O ' 2 = 64 + x 2
và O O ' 2 = 16 + 4 x 2
=> x = 4 => OO' = 80 cm

a: Gọi AH là tiếp tuyến chung của hai đường tròn (O) và (O'), H∈MN
Xét (O) có
HM,HA là các tiếp tuyến
Do đó: HM=HA và HO là phân giác của góc MHA
Xét (O') có
HA,HN là các tiếp tuyến
Do đó: HA=HN và HO' là phân giác của góc AHN
Ta có: HM=HA
HN=HA
Do đó: HM=HN
=>H là trung điểm của MN
Xét ΔAMN có
AH là đường trung tuyến
\(AH=\dfrac{MN}{2}\)
Do đó: ΔAMN vuông tại A
=>\(\widehat{MAN}=90^0\)
b: HO là phân giác của góc MHA
=>\(\widehat{MHA}=2\cdot\widehat{OHA}\)
HO' là phân giác của góc AHN
=>\(\widehat{AHN}=2\cdot\widehat{AHO'}\)
Ta có: \(\widehat{MHA}+\widehat{NHA}=180^0\)(hai góc kề bù)
=>\(2\cdot\left(\widehat{OHA}+\widehat{O'AH}\right)=180^0\)
=>\(2\cdot\widehat{OHO'}=180^0\)
=>\(\widehat{OHO'}=90^0\)
Xét ΔHO'O vuông tại H có HA là đường cao
nên \(HA^2=OA\cdot O'A\)
=>\(HA^2=9\cdot4=36\)
=>\(HA=\sqrt{36}=6\left(cm\right)\)
MN=2*HA
=>MN=2*6=12(cm)

a) Theo tính chất hai tiếp tuyến cắt nhau ta được IA = IB, IA = IC .
Tam giác ABC có đường trung tuyến \(AI=\frac{1}{2}BC\)nên là tam giác vuông
Vậy \(\widehat{BAC}=90^o\left(đpcm\right)\)
b) Theo tính chất hai tiếp tuyến cắt nhau ta có IO, IO' là các tia phân giác của hai góc kề bù AIB, AIC nên :
\(\widehat{OIO'}=\widehat{OIA}+\widehat{O'IA}=\frac{1}{2}\widehat{AIB}+\frac{1}{2}\widehat{AIC}=\frac{1}{2}\left(\widehat{AIB}+\widehat{AIC}\right)\)
Vậy : \(\widehat{OIO'}=90^o\)
c) \(\Delta OIO'\) vuông tại A có IA là đường cao nên theo hệ thức giữa cạnh và đường cao ta có:
IA2 = AO.AO' = 9 . 4 = 36
=> IA = 6 ( cm )
Vậy BC = 2 . IA = 2 . 6 = 12 (cm)

a: Ta có:(O) và (O') tiếp xúc ngoài tại A
=>A nằm giữa O và O'
=>B,O,A,O',C thẳng hàng
=>BA và CA lần lượt là đường kính của (O) và (O')
Kẻ tiếp tuyến chung AI của (O) và (O'), I\(\in\)DE
Xét (O) có
ID,IA là các tiếp tuyến
Do đó: ID=IA
Xét (O') có
IA,IE là các tiếp tuyến
Do đó: IA=IE
Ta có: ID=IA
IA=IE
Do đó: ID=IE
=>I là trung điểm của DE
Xét ΔADE có
AI là đường trung tuyến
AI=1/2DE
Do đó: ΔADE vuông tại A
=>\(\widehat{DAE}=90^0\)
b: Xét (O) có
ΔADB nội tiếp
AB là đường kính
Do đó: ΔADB vuông tại D
=>AD\(\perp\)MB tại D
Xét (O') có
ΔAEC nội tiếp
AC là đường kính
Do đó: ΔAEC vuông tại E
=>AE\(\perp\)MC tại E
Xét tứ giác MDAE có \(\widehat{MDA}=\widehat{MEA}=\widehat{DAE}=90^0\)
nên MDAE là hình chữ nhật
c: ta có: MDAE là hình chữ nhật
=>MA cắt DE tại trung điểm của mỗi đường
mà I là trung điểm của DE
nên I là trung điểm của MA
=>MA\(\perp\)BC tại A
=>MA là tiếp tuyến chung của (O) và (O')
