Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Ta thấy \(\widehat{OAH}+\widehat{HAI}=\widehat{OAI}=90^o\) và \(\widehat{O'AI}+\widehat{IAH}=\widehat{O'AH}=90^o\)
nên \(\widehat{OAH}=\widehat{O'AI}\Rightarrow\widehat{AOH}=\widehat{AO'I}\left(1\right)\)
Ta thấy \(\widehat{OAO'}+\widehat{HAI}=\widehat{OAH}+\widehat{HAI}+\widehat{IAO'}+\widehat{HAI}=\widehat{OAI}+\widehat{HAO'}\)
\(=90^o+90^o=180^o\)
Xét tứ giác AHKI ta cũng có \(\widehat{HKI}+\widehat{HAI}=180^o\Rightarrow\widehat{HKI}=\widehat{OAO'}\left(2\right)\)
Từ (1) và (2) suy ra tứ giác OAO'K là hình bình hành (Có các góc đối bằng nhau)
b) Gọi AJ và AJ' là hai đường kính của đường tròn (O) và (O')
Trước hết, ta có J, B, J' thẳng hàng. Thật vậy: \(\widehat{ABJ}+\widehat{ABJ'}=90^o+90^o=180^o\)
Ta chứng minh J, K ,J' cũng thẳng hàng.
Xét tam giác AJJ' có O' là trung điểm AJ', O'K // AJ, O'K = 1/2AJ
Vậy nên K là trung điểm JJ'.
Tóm lại J, B, K ,J' thẳng hàng.Vậy thì \(\widehat{ABK}=\widehat{ABJ'}=90^o\) hay \(KB\perp BA\)
Hình vẽ như trên
a) Ta thấy ^OAH+^HAI=^OAI=90o và ^O'AI+^IAH=^O'AH=90o
nên ^OAH=^O'AI⇒^AOH=^AO'I(1)
Ta thấy ^OAO'+^HAI=^OAH+^HAI+^IAO'+^HAI=^OAI+^HAO'
=90o+90o=180o
Xét tứ giác AHKI ta cũng có ^HKI+^HAI=180o⇒^HKI=^OAO'(2)
Từ (1) và (2) suy ra tứ giác OAO'K là hình bình hành (Có các góc đối bằng nhau)
b) Gọi AJ và AJ' là hai đường kính của đường tròn (O) và (O')
Trước hết, ta có J, B, J' thẳng hàng. Thật vậy: ^ABJ+^ABJ'=90o+90o=180o
Ta chứng minh J, K ,J' cũng thẳng hàng.
Xét tam giác AJJ' có O' là trung điểm AJ', O'K // AJ, O'K = 1/2AJ
Vậy nên K là trung điểm JJ'.
\(\Rightarrow\) J, B, K ,J' thẳng hàng.Vậy thì ^ABK=^ABJ'=90o hay KB⊥BA

a: Vì ΔABC vuông tại A
nên A nằm trên (O)
b: ΔOAC cân tại O
mà OI là đường cao
nên OI là phân giác của gócc AOC
Xét ΔOAE và ΔOCE có
OA=OC
góc AOE=góc COE
OE chung
Do đó: ΔOAE=ΔOCE
=>góc OCE=90 độ
=>EC là tiếp tuyến của (O)

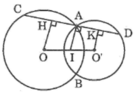
Kẻ OH ⊥ CD, O’K ⊥ CD
Ta có: IA ⊥ CD
Suy ra : OH // IA // O’K
Theo giả thiết : IO = IO’
Suy ra : AH = AK (tính chất đường thẳng song song cách đều) (1)
Ta có : OH ⊥ AC
Suy ra : HA = HC = (1/2).AC (đường kính dây cung) ⇒ AC = 2AH (2)
Lại có : O’K ⊥ AD
Suy ra : KA = KD = (1/2).AD (đường kính dây cung) ⇒ AD = 2AK (3)
Từ (1), (2) và (3) suy ra: AC = AD

Gọi giao điểm của AK và MB là I; giao điểm của IF với AB là J.
Xét tam giác vuông ICA ta thấy DA = DC nên DA = DC = DI.
Lại có DB là trung trực của AF nên DA = DF. Vậy thì DA = DF = DI hay tam giác IFA vuông tại F, suy ra DB // IJ.
Vậy thì DB là đường trung bình tam giác AIJ hay B là trung điểm AJ.
Ta có KF // AJ nên áp dụng Ta let ta có:
\(\frac{KM}{AB}=\frac{IM}{IB}=\frac{MF}{BJ}\)
Do AB = BJ nên KM = MF.
