K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
T
0
DA
1
HL
1
25 tháng 9 2021
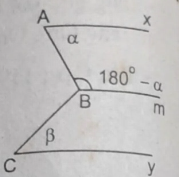
a) Ta có: \(\alpha+\widehat{ABm}=\alpha+180^0-\alpha=180^0\)
Mà 2 góc này là 2 góc trong cùng phía
=> Ax//Bm
b) Trên tia đối Bm kẻ Bn
=> Bn//Ax
\(\Rightarrow\alpha=\widehat{ABn}\)(so le trong)
\(\Rightarrow\widehat{CBn}=\widehat{ABC}-\widehat{ABn}=\alpha+\beta-\alpha=\beta\)
\(\Rightarrow\widehat{CBn}=\widehat{BCy}=\beta\)
Mà 2 góc này là 2 góc so le trong
=> Cy//Bm
CM
22 tháng 1 2017
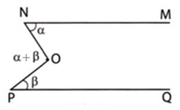
Ta biết rằng nếu hai góc trong cùng phía thì nhau thì hai đường thẳng song song.
B A x ^ + A B y ^ = α + 4 α = 5 α . N ế u 5 α =180 0 , t h ì α =36 0 thì Ax ∥ By
CM
28 tháng 4 2019
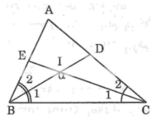
Trong ΔBIC có: ∠(BIC) + ∠B1 + ∠C1 = 180o (tổng 3 góc trong tam giác)
Suy ra: ∠B1 + ∠C1 = 180o - ∠(BIC)
Ta có:
∠B1 = 1/2 ∠B (vì BD là tia phân giác)
∠C1 = 1/2 ∠C (vì CE là tia phân giác)
Suy ra: ∠B + ∠C = 2(∠B1 + ∠C1) = 2.(180o - ∠(BIC))
Trong ΔABC có: ∠A + ∠B + ∠C = 180o (tổng ba góc trong tam giác)
Suy ra: ∠A = 180o - (∠B + ∠C) = 180o - 2.(180o - ∠(BIC)) = 2. ∠(BIC) – 180o
∠(BIC) = α thì ∠A = 2.α – 180o.