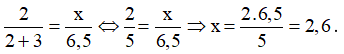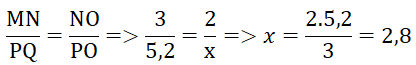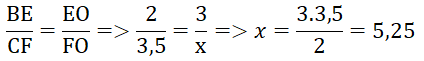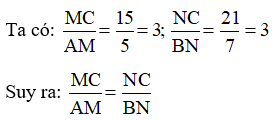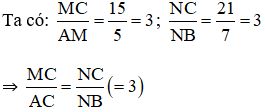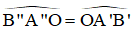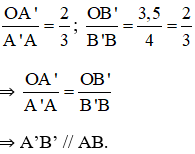K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
H
4
LM
18 tháng 1 2019
Lời giải
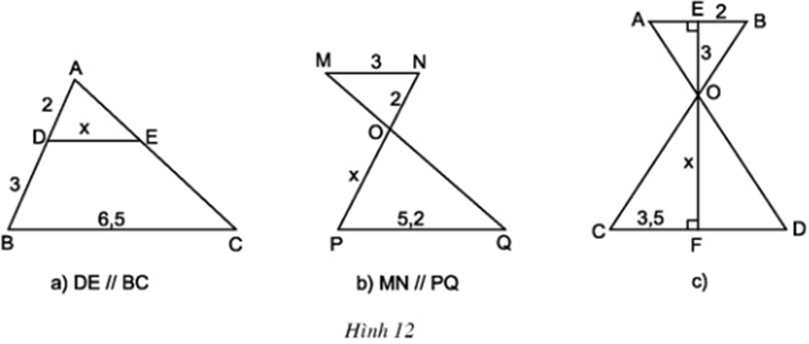
Áp dụng định lí Ta – lét ta có:
- Hình a:
- Hình b:
- Hình c:
18 tháng 1 2019
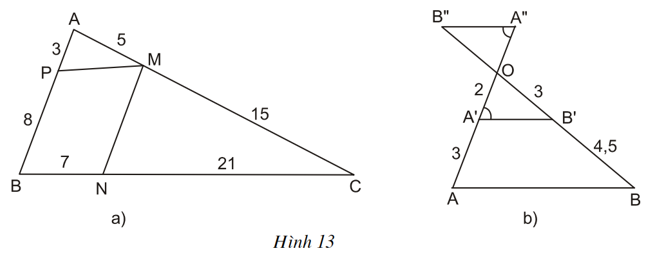
Bài 6 (trang 62 SGK Toán 8 tập 2): Tìm các cặp đường thẳng song song trong hình 13 và giải thích vì sao chúng song song.
Lời giải:
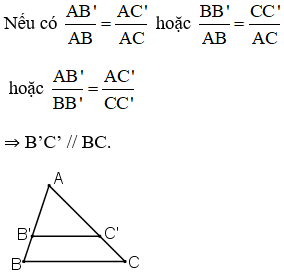
a) Xét hình 13a) : MN // AC.
⇒ MN // AB (Theo định lý Ta-let đảo).
b) Xét hình 13b) : AB // A’B’ // A”B”.
Ta có: 
⇒ A’B’ // A”B” (Hai góc so le trong bằng nhau).
Lại có:
Vậy ta có AB//A’B’//A”B”.
Kiến thức áp dụng
Định lý Ta-let đảo :
+ Nếu một đường thẳng cắt hai cạnh của một tam giác và định ra trên hai cạnh này những đoạn thẳng tương ứng tỉ lệ thì đường thẳng đó song song với cạnh còn lại của tam giác.
ΔABC, B’ ∈ AB, C’ ∈ AC.
27 tháng 8 2021
Bài 10:
a: Thay x=3 vào A, ta được:
\(A=\left(\dfrac{1}{3+2}+\dfrac{1}{3^2-4}\right)=\dfrac{1}{5}+\dfrac{1}{5}=\dfrac{2}{5}\)
b: Ta có: P=AB
\(=\left(\dfrac{1}{x+2}+\dfrac{1}{x^2-4}\right)\cdot\dfrac{x^2+2x}{x-1}\)
\(=\dfrac{x-2+1}{\left(x+2\right)\left(x-2\right)}\cdot\dfrac{x\left(x+2\right)}{x-1}\)
\(=\dfrac{x-1}{x-2}\cdot\dfrac{x}{x-1}\)
\(=\dfrac{x}{x-2}\)
c: Để \(P=\dfrac{2}{3}\) thì \(\dfrac{x}{x-2}=\dfrac{2}{3}\)
\(\Leftrightarrow3x=2x-4\)
hay x=-4(nhận)
AY
0
BT
18 tháng 12 2017
n3-2n2+n=n3-2n2+n-2+2 = n2(n-2)+(n-2)+2=(n-2)(n2+1)+2
Nhận thấy: (n-2)(n2+1) chia hết cho n-2 với mọi n
=> Để biểu thức chia hết cho n-2 thì 2 phải chia hết cho n-2 => n-2=(-2,-1,1,2)
| n-2 | -2 | -1 | 1 | 2 |
| n | 0 | 1 | 3 | 4 |
Đáp số: n=(0,1,3,4)
TN
28 tháng 7 2017
A= (x^2+2x)^2+9x^2+18x+20
=x^4+4x^4+4x^2+9x^2+18x+20
=5x^4+13x^2+18x+20
Cái bài này bạn yêu cầu không rõ nên mình chỉ giúp bạn được bấy nhiêu thôi. Nếu bạn yêu cầu rút gọn thì như trên còn yêu câu khác thì mình chưa chắc nên bạn phải ghi cụ thể nha.
ML
1
7 tháng 10 2021
\(\left(x^2+2x\right)^2-2x^2-4x=3\)
\(\Rightarrow x^4+4x^3+4x^2-2x^2-4x=3\)
\(\Rightarrow x^4+4x^3+2x^2-4x-3=0\)
\(\Rightarrow x^3\left(x-1\right)+5x^2\left(x-1\right)+7x\left(x-1\right)+3\left(x-1\right)=0\)
\(\Rightarrow\left(x-1\right)\left(x^3+5x^2+7x+3\right)=0\)
\(\Rightarrow\left(x-1\right)\left[x^2\left(x+1\right)+4x\left(x+1\right)+3\left(x+1\right)\right]=0\)
\(\Rightarrow\left(x-1\right)\left(x+1\right)\left(x^2+4x+3\right)=0\)
\(\Rightarrow\left(x-1\right)\left(x+1\right)\left[x\left(x+3\right)+\left(x+3\right)\right]=0\)
\(\Rightarrow\left(x-1\right)\left(x+1\right)\left(x+3\right)\left(x+1\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}x=1\\x=-1\\x=-3\end{matrix}\right.\)
28 tháng 8 2021
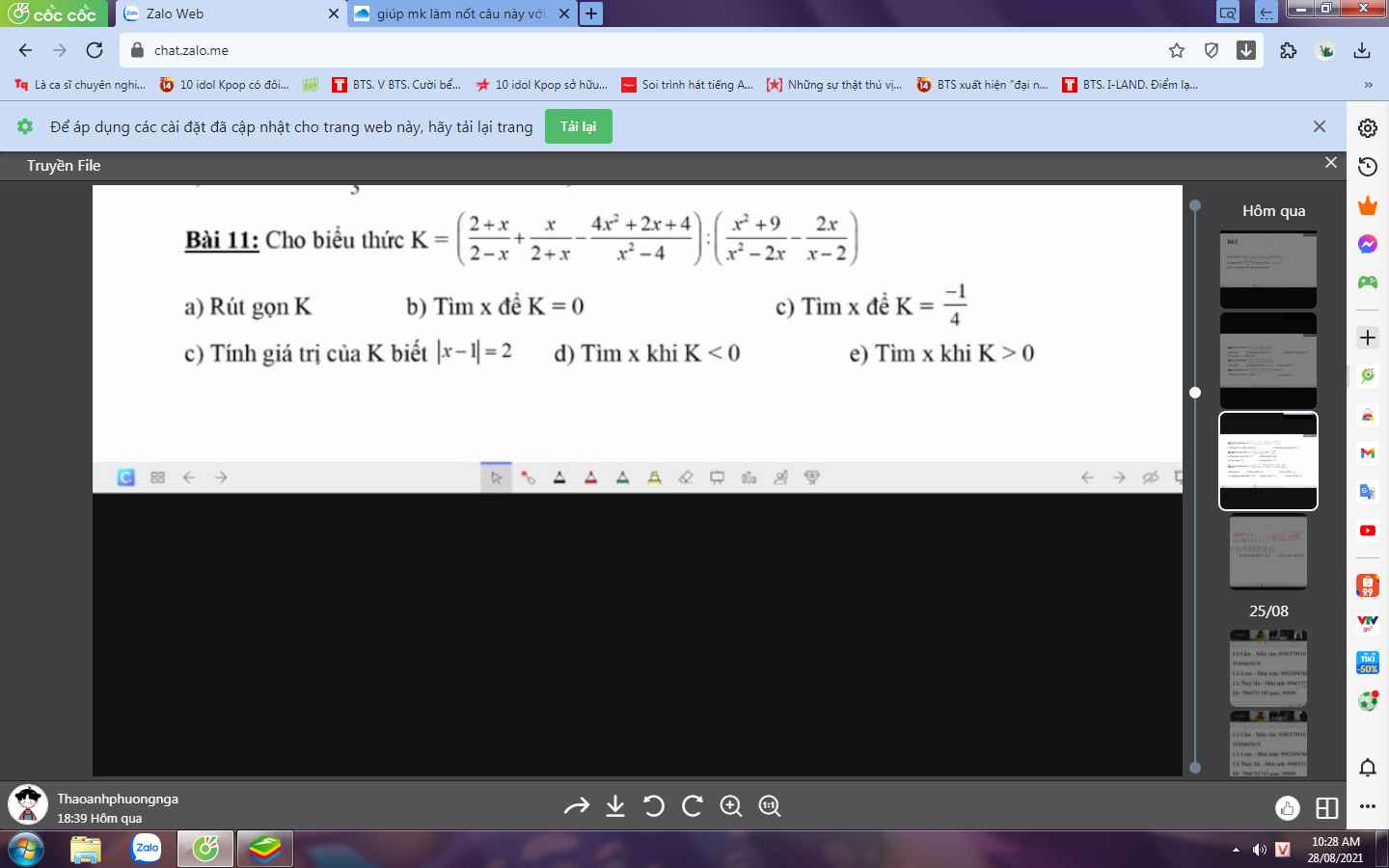
a: Ta có: \(K=\left(\dfrac{2+x}{2-x}+\dfrac{x}{2+x}-\dfrac{4x^2+2x+4}{x^2-4}\right):\left(\dfrac{x^2+9}{x^2-2x}-\dfrac{2x}{x-2}\right)\)
\(=\dfrac{-x^2-4x-4+x^2-2x-4x^2-2x-4}{\left(x-2\right)\left(x+2\right)}:\dfrac{x^2+9-2x^2}{x\left(x-2\right)}\)
\(=\dfrac{-4x^2-8x-8}{\left(x-2\right)\left(x+2\right)}\cdot\dfrac{x\left(x-2\right)}{-x^2+9}\)
\(=\dfrac{-4\left(x^2+2x+1\right)}{x+2}\cdot\dfrac{x}{-\left(x-3\right)\left(x+3\right)}\)
\(=\dfrac{-4x\left(x+1\right)^2}{-\left(x-3\right)\left(x+3\right)\left(x+2\right)}\)