Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(\left\{{}\begin{matrix}SB\perp\left(ABCD\right)\Rightarrow SB\perp AB\\AB\perp BC\end{matrix}\right.\) \(\Rightarrow AB\perp\left(SBC\right)\)
\(\left\{{}\begin{matrix}SC\in\left(SBC\right)\\AB\perp\left(SBC\right)\end{matrix}\right.\) \(\Rightarrow AB\perp SC\)

\(\left\{{}\begin{matrix}SB\perp\left(ABCD\right)\Rightarrow SB\perp BC\\BC\perp AB\end{matrix}\right.\) \(\Rightarrow BC\perp\left(SAB\right)\)
\(\left\{{}\begin{matrix}BC\perp\left(SAB\right)\\SA\in\left(SAB\right)\end{matrix}\right.\) \(\Rightarrow BC\perp SA\)

a/ Ta có: \(SA\perp\left(ABCD\right)\Rightarrow SA\perp BD\)
Mà \(BD\perp AC\) (hai đường chéo hình thoi)
\(\Rightarrow BD\perp\left(SAC\right)\)
c/ Do \(SA\perp\left(ABCD\right)\Rightarrow AC\) là hình chiếu của SC lên (ABCD)
\(\Rightarrow\widehat{SCA}\) là góc giữa SC và (ABCD)
\(\widehat{ABC}=60^0\Rightarrow\Delta ABC\) đều \(\Rightarrow AC=a\)
\(tan\widehat{SCA}=\frac{SA}{AC}=\frac{a\sqrt{3}}{a}=\sqrt{3}\)
\(\Rightarrow\widehat{SCA}=60^0\)

Ta có:
\(\left\{{}\begin{matrix}SA\perp\left(ABCD\right)\Rightarrow SA\perp BD\\AC\perp BD\left(\text{hai đường chéo hình vuông}\right)\end{matrix}\right.\) \(\Rightarrow BD\perp\left(SAC\right)\)
b.
Do \(SA\perp\left(ABCD\right)\Rightarrow AC\) là hình chiếu vuông góc của SC lên (ABCD)
\(\Rightarrow\widehat{SCA}\) là góc giữa SC và (ABCD)
\(AC=\sqrt{AB^2+BC^2}=a\sqrt{2}\)
\(tan\widehat{SCA}=\dfrac{SA}{AC}=\dfrac{a\sqrt{2}}{a\sqrt{2}}=1\)
\(\Rightarrow\widehat{SCA}=45^0\)

1: BC vuông góc AB
BC vuông góc SA
=>BC vuông góc (SAB)
BD vuông góc CA
BD vuông góc SA
=>BD vuông góc (SAC)
2: DC vuông góc AD
DC vuông góc SA
=>DC vuông góc (SAD)
=>(SCD) vuông góc (SAD)
4: (SC;(SAB))=(SC;SB)=góc CSB
\(AC=\sqrt{a^2+a^2}=a\sqrt{2}\)
\(SC=\sqrt{AC^2+SA^2}=a\sqrt{5}\)
\(SB=\sqrt{SA^2+AB^2}=2a\)
BC=a
Vì SB^2+BC^2=SC^2
nên ΔSCB vuông tại B
sin CSB=BC/SC=1/căn 5
=>góc CSB=27 độ
3: BC vuông góc SAB
=>AE vuông góc BC
mà AE vuông góc SB
nên AE vuông góc (SBC)
=>AE vuông góc SC
4: (SB;(SAC))=(SB;SD)=góc DSB
\(SD=\sqrt{SA^2+AD^2}=2a;SB=2a;DB=a\sqrt{2}\)
\(cosDSB=\dfrac{4a^2+4a^2-2a^2}{2\cdot2a\cdot2a}=\dfrac{3}{4}\)
=>góc DSB=41 độ

a.
\(\Delta_VSAB=\Delta_VSAD\left(c.g.c\right)\Rightarrow AB_1=AD_1\)
\(\Rightarrow SB_1=SD_1\Rightarrow\dfrac{SB_1}{SB}=\dfrac{SD_1}{SD}\)
\(\Rightarrow B_1D_1||BD\) (Talet đảo)
\(\left\{{}\begin{matrix}SA\perp\left(ABCD\right)\Rightarrow SA\perp BC\\BC\perp AB\end{matrix}\right.\) \(\Rightarrow BC\perp\left(SAB\right)\Rightarrow BC\perp AB_1\)
\(\Rightarrow AB_1\perp\left(SBC\right)\Rightarrow AB_1\perp SC\)
Hoàn toàn tương tự: \(AD_1\perp\left(SCD\right)\Rightarrow AD_1\perp SC\)
\(\Rightarrow SC\perp\left(AB_1D_1\right)\)
b.
\(\left\{{}\begin{matrix}SC\perp AC_1\\SC\perp\left(AB_1D_1\right)\end{matrix}\right.\) \(\Rightarrow AC_1\in\left(AB_1D_1\right)\)
\(\Rightarrow\) 4 điểm \(A;B_1;C_1;D_1\) đồng phẳng
Theo chứng minh câu a, \(AB_1\perp\left(SBC\right)\Rightarrow AB_1\perp B_1C_1\) (1)
\(AD_1\perp\left(SCD\right)\Rightarrow AD_1\perp\left(D_1C_1\right)\)
\(\Rightarrow B_1;D_1\) cùng nhìn \(AC_1\) dưới 1 góc vuông nên tứ giác \(AB_1C_1D_1\) nội tiếp đường tròn đường kính \(AC_1\)
c.
Gọi E là trung điểm BC
\(\Rightarrow C_1E\) là đường trung bình tam giác SBC
\(\Rightarrow C_1E||SB\Rightarrow\widehat{SB;AC_1}=\widehat{\left(C_1E;AC_1\right)}=\widehat{AC_1E}\)
\(SB=\sqrt{SA^2+AB^2}=a\sqrt{3}\)
\(C_1E=\dfrac{1}{2}SB=\dfrac{a\sqrt{3}}{2}\)
\(AE=\sqrt{AB^2+BE^2}=\sqrt{AB^2+\left(\dfrac{BC}{2}\right)^2}=\dfrac{a\sqrt{5}}{2}\)
\(\dfrac{1}{AC_1^2}=\dfrac{1}{SA^2}+\dfrac{1}{AC^2}\Rightarrow AC_1=\dfrac{SA.AC}{\sqrt{SA^2+AC^2}}=a\)
Áp dụng định lý hàm cos cho tam giác \(AEC_1\):
\(cos\widehat{AC_1E}=\dfrac{AC_1^2+C_1E^2-AE^2}{2AC_1.C_1E}=0\Rightarrow\widehat{AC_1E}=90^0\)

1: BC vuông góc AB
BC vuông góc SA
=>BC vuông góc (SAB)
BD vuông góc CA
BD vuông góc SA
=>BD vuông góc (SAC)
2: DC vuông góc AD
DC vuông góc SA
=>DC vuông góc (SAD)
=>(SCD) vuông góc (SAD)
4: (SC;(SAB))=(SC;SB)=góc CSB
\(AC=\sqrt{a^2+a^2}=a\sqrt{2}\)
\(SC=\sqrt{AC^2+SA^2}=a\sqrt{5}\)
\(SB=\sqrt{SA^2+AB^2}=2a\)
BC=a
Vì SB^2+BC^2=SC^2
nên ΔSCB vuông tại B
sin CSB=BC/SC=1/căn 5
=>góc CSB=27 độ
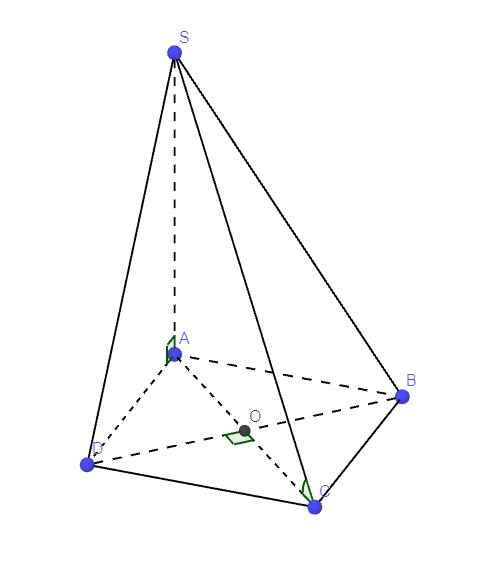

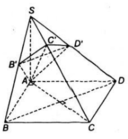


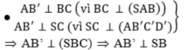
Ta có: \(\left\{{}\begin{matrix}SA\perp\left(ABCD\right)\Rightarrow SA\perp BD\\BD\perp AC\left(\text{hai đường chéo hình vuông}\right)\end{matrix}\right.\) \(\Rightarrow BD\perp\left(SAC\right)\)
\(\left\{{}\begin{matrix}BD\perp\left(SAC\right)\\SC\in\left(SAC\right)\end{matrix}\right.\) \(\Rightarrow BD\perp SC\)