


Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.






Áp dụng định lí cosin trong tam giác ABC ta có:
\(B{C^2} = A{C^2} + A{B^2} - 2AC.AB.\cos A\)
\(\begin{array}{l} \Leftrightarrow B{C^2} = 7,{5^2} + 3,{5^2} - 2.7,5.3,5.\cos {135^o}\\ \Leftrightarrow B{C^2} \approx 105,6\\ \Leftrightarrow BC \approx 10,3\end{array}\)
Áp dụng định lí sin trong tam giác ABC ta có: \(\frac{{BC}}{{\sin A}} = 2R\)
\( \Rightarrow R = \frac{{BC}}{{2.\sin A}} = \frac{{10,3}}{{2.\sin {{135}^o}}} \approx 7,3\)

\(cosA=\dfrac{AB^2+AC^2-BC^2}{2AB.AC}=-\dfrac{1}{32}\)
\(\Rightarrow A\approx92^0\)
\(p=\dfrac{AB+AC+BC}{2}=\dfrac{31}{2}\)
\(S_{ABC}=\sqrt{p\left(p-AB\right)\left(p-AC\right)\left(p-BC\right)}\simeq40\)
\(r=\dfrac{S}{p}=\dfrac{80}{31}\)

a, Vec-tơ AB=(-3;4) => vtpt của đường thẳng AB là (4;3)
Pt AB: 4(x-2)+3(y-2)=0 <=> 4x+3y-14=0
Pt AC và BC làm tương tự
b, Đường cao AH có vtpt là vecto BC=(-4;-3) hay =(4;3)
Pt đường cao AH: 4(x-2)+3(y-2)=0 <=> 4x+3y-14=0
c) ta có độ dài đoạn AB= căn của (-1+2)^2+(6-2)^2 =5
" " BC= căn của (-5+1)^2+(3-6)^2 =5
==> Tan giác ABC cân tại B (1)
lại có véc tơ AB=(-3;4), véc tơ BC=(-4;-3) =>véc tơ AB*BC =(-3)*4+(-4)*(-3) =0
===>tam giác vuông tại B (2)
từ (1,2) ==> tam giác ABC vuông cân

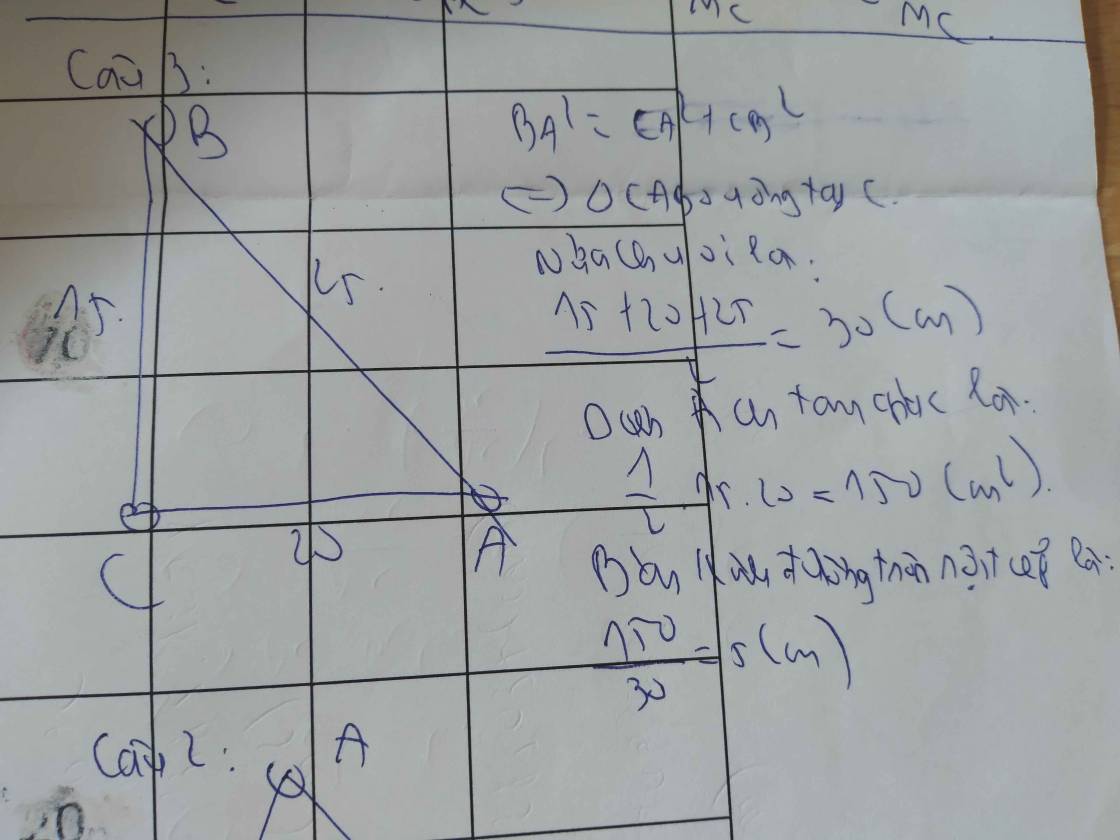
Xét tam giác ABC có đường cao BH:
cos ABC = \(\dfrac{7^2+15^2-13^2}{2\cdot7\cdot15}\) = \(\dfrac{1}{2}\) \(\Rightarrow\) \(\widehat{ABC}=60^o\)
\(p=\dfrac{13+7+15}{2}=17,5\) (cm)
Hê-rông: \(S=\sqrt{17,5\cdot\left(17,5-13\right)\cdot\left(17,5-7\right)\cdot\left(17,5-15\right)}\approx45,5\) (cm2)
\(S=\dfrac{abc}{4R}\) \(\Rightarrow\) \(R=\dfrac{abc}{4S}\approx\dfrac{13\cdot7\cdot15}{4\cdot45,5}=7,5\) (cm)
\(S=\dfrac{1}{2}BH\cdot AC\) \(\Rightarrow\) \(BH=\dfrac{2S}{AC}\approx\dfrac{2\cdot45,5}{13}=7\) (cm)
Chúc bn học tốt!