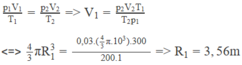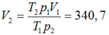Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có
Trạng thái 1 { V 1 = 200 l p 1 T 1 = 27 + 273 = 300 K Trạng thái 2 { V 2 = ? p 2 = 0 , 8 p 1 T 2 = 273 + 17 = 290 K
Áp dụng
p 1 V 1 T 1 p 2 V 2 T 2 ⇒ V 2 = p 1 V 1 T 2 p 2 T 1 = p 1 .200.290 0 , 5 p 1 .300 V 2 = 241 , 67 ( l )

Mỗi lần bơm, người ta đưa được vào trong túi cao su một lượng không khí có thể tích
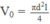
áp suất p 0 = 1 atm.
Khi được bơm vào túi ở áp suất p = 4 atm, lượng không khí này có thể tích V. Vì nhiệt độ không đổi nên:
pV = p 0 V 0 ⇒ V = 0,157. 10 - 3 m 3
Số lần bơm: n = (6,28. 10 - 3 )/(0,157. 10 - 3 ) = 40

Đáp án C
Xét khối khí trong bóng sau 12 lần bơm. Trước khi bơm vào bóng, khối khí đó có thể tích là: V0=12.0,125+2,5=4 l và áp suất của khối khí đó ban đầu là P0 = 1atm. Sau khi bơm vào bóng thể tích của khối khí đó là V = 2,5l và áp suất của quá trình đó là P
Vì nhiệt độ là không đổi trong suốt quá trình bơm, do đó áp dụng định luật Bôi-lơ-ma-ri-ốt, ta có:
![]()
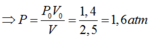

Xét quá trình biến đổi của lượng không khí được bơm vào quả bóng
TH1 { v 1 = 125.40 = 5000 c m 3 = 5 l p 1 = p 0 = 10 5 N / m 2
TH2 { v 2 = 2 , 5 l p 2 = ?
p 1 v 1 = p 2 v 2 ⇒ p 2 = p 1 v 1 v 2 = 10 5 .5 2 , 5 = 2.10 5 N / m 2

\(T_1=20^oC=293K\)
\(T_2=42^oC=315K\)
Áp suất săm xe khi để ở nhiệt độ \(42^oC\). Quá trình đẳng tích:
\(\dfrac{p_1}{T_1}=\dfrac{p_2}{T_2}\Rightarrow\dfrac{2}{293}=\dfrac{p_2}{315}\)
\(\Rightarrow p_2=2,15atm< p_{max}=2,5atm\)
Vậy săm xe không bị nổ.