Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Câu 5: Từ các số 1, 2, 3, 4, 5, 6 hỏi có thể lập được bao nhiêu số tự nhiên chẵn có ba chữ số đôi một khác nhau?
A. 108
B. 90
C. 120
D. 60
Câu 5: Từ các số 1, 2, 3, 4, 5, 6 hỏi có thể lập được bao nhiêu số tự nhiên chẵn có ba chữ số đôi một khác nhau?
A. 108
B. 90
C. 120
D. 60

Bài 1:Cho A={0;1;2;3;4;5}.Hỏi có thể lập được bao nhiêu số có 4 chữ số khác nhau sao cho tổng hai chữ số đầu nhỏ hơn tổng hai chữ số sau 1 đơn vị
Bài 2:Với các chữ số 1;2;3;4;5;6 có thể lập được bao nhiêu số tự nhiên thỏa mãn?
a,gồm có 6 chữ số
b,gồm có 6 chữ số khác nhau
c,gồm có 6 chữ số và chia hết cho 2
Bài 3:Cho X={0;1;2;3;4;5;6}
a,Có bao nhiêu số chẵn có 4 chữ số khác nhau đôi một ?
b,Có bao nhiêu chữ số có 3 chữ số khác nhau chia hết cho 5\
c, Có bao nhiêu số có 3 chữ số khác nhau chia hết cho 9 .
Bài 4:Có bao nhiêu số tự nhiên có tính chất.
a,là số chẵn có 2 chữ số không nhết thiết phải khác nhau
b,là số lẻ và có 2 chữ số không nhất thiết phải khác nhau
c,là số lẻ và có hai chữ số khác nhau
d,là số chẵn và có 2 chữ số khác nhau
Bài 5:Cho tập hợp A{1;2;3;4;5;6}
a,có thể lập được bao nhiêu số gồm 4 chữ số khác nhau hình thành từ tập A
b,có thể lập được bao nhiêu số gồm 3 chữ số khác nhau và chia hết cho 2
c,có thể lập được bao nhiêu số gồm 5 chữ số khác nhau và chia hết cho 5
dài quá
botay.com.vn

Các số là:
2035;2053;2305;2350;2503;2530;3025;3052;3205;3250;3502;3520;5023;5032;5203;5230;5302;5320
2035+2053+2305+2350+2503+2530+3025+3052+3205+3250+3502+3520+5023+5032+5203+5230+5302+5320=44563

Sơ đồ con đường |
Lời giải chi tiết |
|
Gọi số cần lập có dạng a b c ¯ .
Từ a b c ¯ ⋮ 5 ⇒ c = 5 , ta có a b 5 ¯ . Từ a b 5 ¯ ⋮ 3 ⇒ a + b + 5 ⋮ 3 suy ra tồn tại những cặp a ; b là 1 ; 3 ; 1 ; 6 ; 3 ; 4 ; 4 ; 6 Hơn nữa, a và b bình đẳng nên có tổng cộng: 4.2=8 số tìm được. |

Bài 1 :
a) => Ta có dãy : 1,2,3,...,19
Vậy có số số tự nhiên nhỏ hơn 20 là:
(19-1):1+1 = 19 số
b) với n là vô hạn
c) với n là vô hạn
Bài 2 :
Ta có abc là chính
=> có thể lập các cách sau :
+ abc , acb
+ bac , bca
+ cab , cba
Vậy có thể lập được 6 số có 3 chữ số như vậy
bài 3 : gọi 5 chữ số đó là abcde
Tương tự bài 2 có thể lập lần lượt các chữ số thay thế đứng đầu :
- Ta có các dạng 3 chữ số như sau : abc , abd , acd , ace , ade , abe ( Tương tự có tất cả 5 chữ số => có 6.5 = 30 dạng tương tự )
- Mà mỗi dạng có thể lập được 3 chữ số
Vậy => 6.30 = 180 số
Bài 4 :
=> + Từ 3 đến 9 cần 7 chữ số
+ Từ 10 đến 99 cần 180 chữ số
+ Từ 100 đến 132 cần 99 chữ số
Vậy cần số chữ số để đánh hết quyển sách đó là :
7+180+99 = 286 chữ số

a, Ta có 9 cách chọn số hàng nghìn
8 cách chọn số hàng trăm
7 cách chọn số hàng chục
6 cách chọn số hàng đơn vị
Vậy số số hạng lập được là :
9 . 8 . 7. 6 = 3024 ( số hạng )
b,Ta có 9 cách chọn số hàng nghìn
9 cách chọn số hàng trăm
9 cách chọn số hàng chục
9 cách chọn số hàng đơn vị
Vậy số số hạng lập được là :
9 . 9 .9 . 9 = 6561 ( số )
c, Tổng các chữ số đã lập ở câu a là :
(1 + 2 + 3 + ... +9). 9 + (1+2+3+...+9).8 + (1+2+3+...+9).7 + (1+2+3+...+9).6
= ( 1+2+3+...+9) . (9+8+7+6)
= 45 . 30
= 1350
Chúc bạn học tốt nha

Sơ đồ con đường |
Lời giải chi tiết |
|
Gọi số có 3 chữ số chia hết cho 3 là a b c - . Khi đó tổng các chữ số là a+b+c chia hết cho 3. Các bộ 3 số thoã mãn điều kiện đó là: 1 ; 3 ; 5 , 1 ; 5 ; 6 , 3 ; 4 ; 5 , 4 ; 5 ; 6 Mỗi bộ 3 lại có: 3 cách chọn hàng trăm. 2 cách chọn hàng chục. 1 cách chọn hàng đơn vị. Có: 3.2.1= 6 cách chọn. Vậy tổng có: 4.6= 24 cách chọn. |

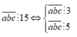
Câu 5: Từ các số 1, 2, 3, 4, 5, 6 hỏi có thể lập được bao nhiêu số tự nhiên chẵn có ba chữ số đôi một khác nhau?
A. 108
B. 90
C. 120
D. 60
Mỗi số cần lập ứng với một chỉnh hợp chập 3 của 6 phần tử
Nên số cần lập là: \(A^3_6=120\) số.