Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: ΔABC cân tại A
mà AH là phân giác
nên H là trung điểm của BC
=>HB=HC
b: Xét ΔHDB vuông tại D và ΔHEC vuông tại E có
HB=HC
góc B=góc C
Do đó: ΔHDB=ΔHEC

a: Xét ΔAHB vuông tại H và ΔAHC vuông tại H có
AB=AC
AH chung
Do đó: ΔAHB=ΔAHC
=>HB=HC
b: Ta có: ΔAHB=ΔAHC
=>\(\widehat{BAH}=\widehat{CAH}\)
Xét ΔADH vuông tại D và ΔAEH vuông tại E có
AH chung
\(\widehat{DAH}=\widehat{EAH}\)
Do đó: ΔADH=ΔAEH
=>AD=AE và HD=HE
Xét ΔABC có \(\dfrac{AD}{AB}=\dfrac{AE}{AC}\)
nên DE//BC
c: Ta có: HD=HF
mà H nằm giữa D và F
nên H là trung điểm của DF
Xét ΔEDF có
EH là đường trung tuyến
\(EH=\dfrac{DF}{2}\)
Do đó: ΔEDF vuông tại E

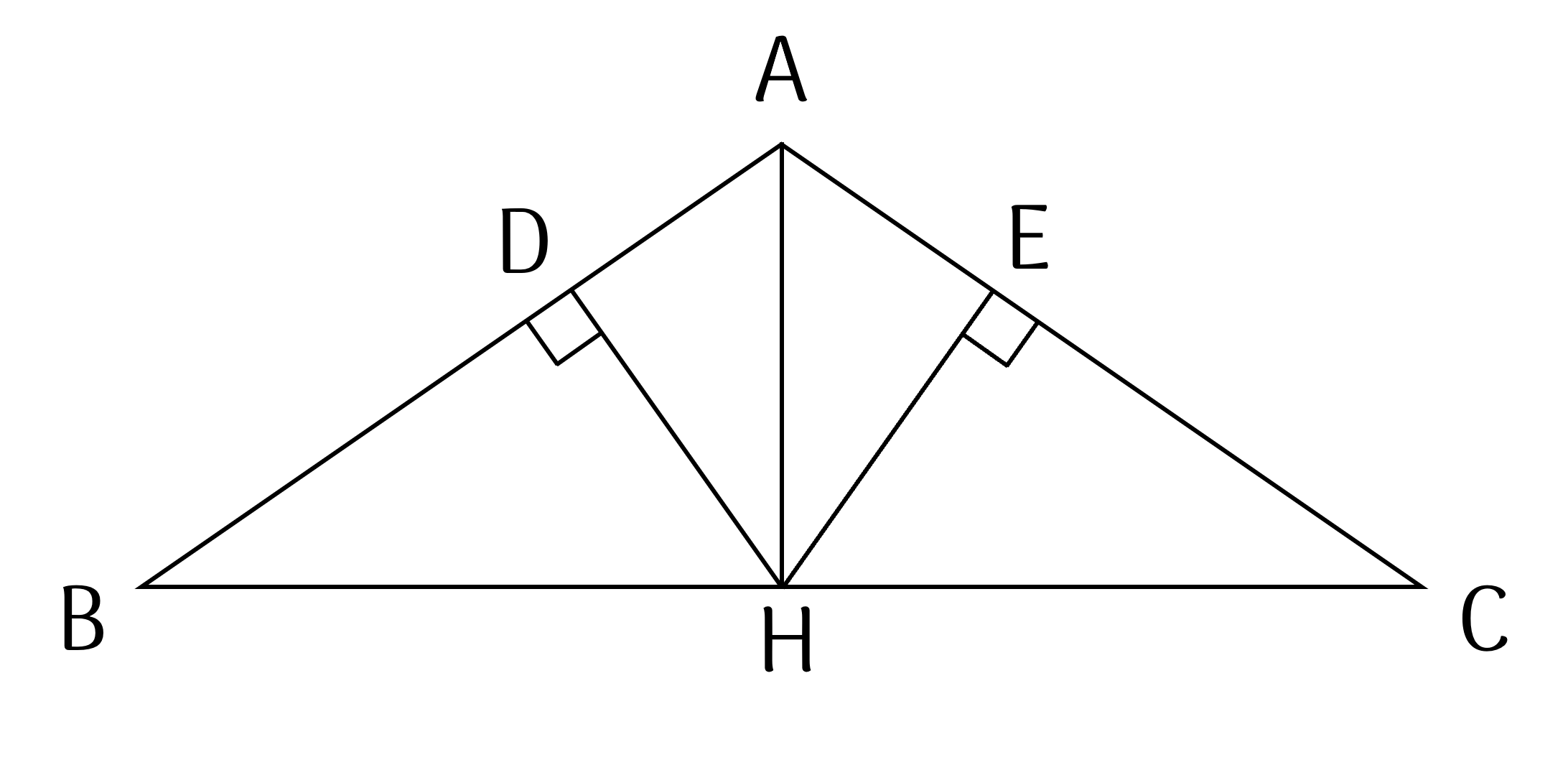
a) Xét hai tam giác vuông $AHB$ và $AHC$ có:
$AH$ là cạnh chung;
$AB = AC$ (gt);
Suy ra $\Delta AHB=\Delta AHC$ (cạnh huyền - cạnh góc vuông)
Suy ra $HB = HC$ (Hai cạnh tương ứng)
$\widehat{BAH} = \widehat{CAH}$ (hai góc tương ứng).
b) Xét hai tam giác vuông $ADH$ và $AEH$ có:
$AH$ là cạnh chung;
$\widehat{BAH} = \widehat{CAH}$ (cmt);
Suy ra $\Delta ADH=\Delta AEH$ (cạnh huyền - góc nhọn).
Suy ra $HD = HE$ (Hai cạnh tương ứng) nên $\Delta HDE$ cân tại $H$.

a: Ta có: ΔABC cân tại A
mà AH là đường cao
nên H là trung điểm của BC
hay HB=HC
Ta có: ΔABC cân tại A
mà AH là đường cao
nên AH là đường phân giác
hay \(\widehat{BAH}=\widehat{CAH}\)
b: BH=CH=BC/2=4(cm)
nên AH=3(cm)
c: Xét ΔAEH vuông tại E và ΔADH vuông tại D có
AH chung
\(\widehat{EAH}=\widehat{DAH}\)
DO đó: ΔAEH=ΔADH
Suy ra: HE=HD
hay ΔHDE cân tại H

a) Xét ΔABH vuông tại H và ΔACH vuông tại H có
AB=AC(ΔABC cân tại A)
AH chung
Do đó: ΔABH=ΔACH(Cạnh huyền-cạnh góc vuông)
Suy ra: HB=HC(Hai cạnh tương ứng) và \(\widehat{BAH}=\widehat{CAH}\)(Hai góc tương ứng)

a) Xét tam giác ABH vuông tại H và tam giác ACH vuông tại H có:
AH: chung
AB=AC (gt)
=>Tam giác ABH=tam giác ACH (cạnh huyền-cạnh góc vuông)
=>HB=HC (2 cạnh tương ứng)
b)Vì HB=HC (câu a) => HB=HC=BC:2=8:2=4 (cm)
Xét tam giác ABH vuông tại H có: AB2 = AH2 + BH2 (định lý Py-ta-go)
52 = AH2 + 42
AH2 = 52 - 42 = 25-16=9
AH=\(\sqrt{9}=3\)
c) Vì tam giác ABH=tam giác ACH (câu a) => góc BAH=góc CAH (2 góc tương ứng)
Xét tam giác ADH vuông tại D và tam giác AEH vuông tại E có:
AH: chung
góc BAH=góc CAH (cmt)
=> Tam giác ADH=tam giác AEH (cạnh huyền-góc nhọn)
=>HD=HE (2 cạnh tương ứng)
=>tam giác DHE cân tại H
d) Tam giác EHC vuông tại E có HC là cạnh huyền =>HC là cạnh lớn nhất trong tam giác EHC hay HC>HE
Mà HE=HD (cmt) => HC>HD

a: Xét ΔAHB vuông tại H và ΔAHC vuông tại H có
AB=AC
AH chung
Do đó: ΔAHB=ΔAHC
b: Xét ΔAHM vuông tại M và ΔAHN vuông tại N có
AH chung
\(\widehat{MAH}=\widehat{NAH}\)
Do đó: ΔAMH=ΔANH
Suy ra: AM=AN
hay ΔAMN cân tại A

a: Xét ΔAHB vuông tại H và ΔAHC vuông tại H có
AB=AC
AH chung
Do đó: ΔAHB=ΔAHC
b: Xét ΔAHM vuông tại M và ΔAHN vuông tại N có
AH chung
\(\widehat{MAH}=\widehat{NAH}\)
Do đó: ΔAMH=ΔANH
Suy ra: AM=AN
hay ΔAMN cân tại A

a.ta có trong tam giác cân ABC đường cao cũng là đường trung tuyến => HB = HC
b.áp dụng định lý pitago ta có:
\(AB^2=AH^2+HB^2\)
\(5^2=AH^2+\left(8:2\right)^2\)
\(AH=\sqrt{5^2-4^2}=3cm\)
c.Xét tam giác vuông BHD và tam giác vuông CHE, có:
BH = CH ( cmt )
góc B = góc C ( ABC cân )
Vậy tam giác vuông BHD = tam giác vuông CHE
=> HD = HE
=> HDE cân tại H
d.ta có AB = AD + DB
AC = AE + EC
Mà BD = CE ( 2 cạnh tương ứng của 2 tam giác bằng nhau )
=> AD = AE
=> ADE cân tại A
Mà A là đường cao cũng là đường trung trực trong tam giác cân ABC cũng là đường trung trực của tam giác cân ADE ( cmx )
Chúc bạn học tốt !!!!
a: Ta có; ΔABC cân tại A
mà AH là đường cao
nên H là trung điểm của BC
b: Xét ΔHDB vuông tại D và ΔHEC vuông tại E có
HB=HC
góc B=góc C
Do đó: ΔHBD=ΔHCE
=>HD=HE
a: Ta có; ΔABC cân tại A
mà AH là đường cao
nên H là trung điểm của BC
b: Xét ΔHDB vuông tại D và ΔHEC vuông tại E có
HB=HC
góc B=góc C
Do đó: ΔHBD=ΔHCE
=>HD=HE