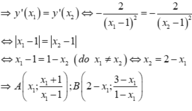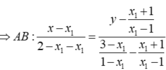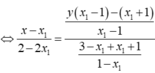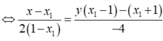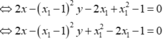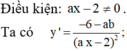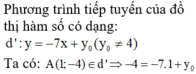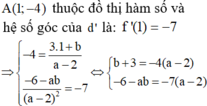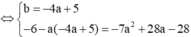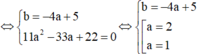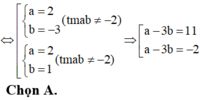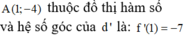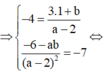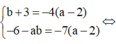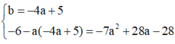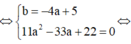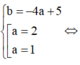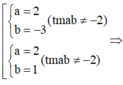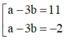Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn A.
Phương trình hoành độ giao điểm của đồ thị (C) và đường thẳng d
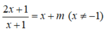
![]()
Khi đó d cắt (C) tại hai điểm phân biệt A; B khi và chi khi phương trình (1) có hai nghiệm phân biệt khác -1.
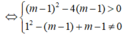
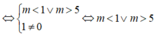
![]()
![]() trong đó x1, x2 là nghiệm của (1) (nên ta có
trong đó x1, x2 là nghiệm của (1) (nên ta có 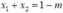 ).
).
Suy ra hệ số góc của các tiếp tuyến tại điểm A và B lần lượt là
![]()
Vì tiếp tuyến tại A và B song song, đồng thời x1 ≠ x2 nên phải có
![]()
suy ra
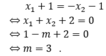
Kết hợp điều kiện ,vậy không có giá trị nào của m thỏa mãn.

+ Phương trình hoành độ giao điểm của đồ thị C và đường thẳng d
2 x + 1 x + 1 = x + m ⇔ x ≠ - 1 x 2 + ( m - 1 ) x + m - 1 = 0 ( 1 )
+ Khi đó d cắt C tại hai điểm phân biệt A; B khi và chi khi phương trình (1) có hai nghiệm phân biệt khác -1
⇔ ( m - 1 ) 2 - 4 ( m - 1 ) > 0 ( - 1 ) 2 - ( m - 1 ) + m - 1 ≠ 0 ⇔ m < 1 ∨ m > 5 ( * )
Khi đó ta lại có A( x1 ; x1+m) ; B( x2 ; x2+ m) ;
A B → = ( x 2 - x 1 ; x 2 - x 1 ) nên A B = 2 ( x 2 - x 1 ) 2 = 2 x 2 - x 1
và x 2 + x 1 = 1 - m x 2 . x 1 = m - 1
Từ đây ta có
A B = 10 ⇔ x 2 - x 1 = 5 ⇔ x 2 + x 1 2 - 4 x 2 x 1 = 5 ⇔ ( 1 - m ) 2 - 4 ( m - 1 ) = 5 ⇔ m 2 - 6 m = 0
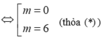
Vậy m= 0 hoặc m= 6.
Chọn D.

Gọi k là hệ số góc của tiếp tuyến tại M, N thì \(x_M;x_N\) là nghiệm của phương trình :
\(f'\left(x\right)=k\Leftrightarrow3x^2-6x-k=0\)
Để tồn tại hai tiếp điểm M, N thì phải có \(\Delta'>0\Leftrightarrow k>-3\)
Ta có \(y=f'\left(x\right)\left(\frac{1}{3}x-\frac{1}{3}\right)-2x+2\)
Từ \(f'\left(x_M\right)=f'\left(x_N\right)=k\) suy ra phương trình đường thẳng MN là :
\(y=\left(\frac{k}{3}-2\right)x+2-\frac{k}{3}\), khi đó \(A\left(1;0\right);B\left(0;\frac{6-k}{3}\right)\)
Ta có \(AB^2=10\Leftrightarrow k=15\) (do k > -3)
Từ đó ta có 2 tiếp tuyến cần tìm là :
\(y=15x-12\sqrt{6}-15\)
\(y=15x+12\sqrt{6}-15\)

Pt hoành độ giao điểm:
\(x^3-6x^2+9x=mx\)
\(\Leftrightarrow x\left(x^2-6x+9-m\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x^2-6x+9-m=0\left(1\right)\end{matrix}\right.\)
Đường thẳng cắt đồ thị tại 3 điểm pb khi và chỉ khi (1) có 2 nghiệm pb khác 0
\(\Leftrightarrow\left\{{}\begin{matrix}9-m\ne0\\\Delta'=9-\left(9-m\right)>0\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}m>0\\m\ne9\end{matrix}\right.\)
Khi đó hoành độ A, B là nghiệm của (1) nên theo hệ thức Viet:
\(x_A+x_B=6\Rightarrow x_I=\dfrac{x_A+x_B}{2}=3\)
\(\Rightarrow\) I luôn nằm trên đường thẳng song song Oy có pt: \(x-3=0\)

Gọi \(A\left(a;\frac{2a}{a-1}\right);B\left(b;\frac{2b}{b-1}\right);\left(a,b\ne0;a,b\ne1;a\ne b\right)\) thuộc đồ thị (C)
Khi đó hệ số góc của các đường tiếp tuyếb rại A; B lần lượt là :
\(k_1=-\frac{2}{\left(a-1\right)^2};k_2=-\frac{2}{\left(b-1\right)^2};\)
Do các đường tiếp tuyến song song nên :
\(-\frac{2}{\left(a-1\right)^2}=-\frac{2}{\left(b-1\right)^2};\)
\(\Leftrightarrow a+b=2\)
Mặt khác, ta có : \(\overrightarrow{OA}=\left(a;\frac{2a}{a-1}\right);\overrightarrow{OB}=\left(b;\frac{2b}{b-1}\right)\)
Do OAB là tam giác vuông tại O nên \(\overrightarrow{OA}.\overrightarrow{OB}=0\Leftrightarrow ab+\frac{4ab}{\left(a-1\right)\left(b-1\right)}=0\)
Ta có hệ : \(\begin{cases}a+b=2\\ab+\frac{4ab}{\left(a-1\right)\left(b-1\right)}=0\end{cases}\)
Giải hệ ta được : \(\begin{cases}a=-1\\b=3\end{cases}\) hoặc \(\begin{cases}a=3\\b=-1\end{cases}\)
Vậy 2 điểm cần tìm có tọa độ là : (-1;1) và (3;3)

Đặt \(A\left(a;a^3-3a^2+2\right);B\left(b;b^3-3b^2+2\right);a\ne b\)
Hệ số góc của tiếp tuyến với (C) tại A, B là :
\(k_A=y'\left(x_A\right)=3a^2-6a;k_B=y'\left(x_B\right)=3b^2-6b\)
Tiếp tuyến của (C) tại A và B song song với nhau khi và chỉ khi \(k_A=k_B\)
\(\Leftrightarrow3a^2-6a=3b^2-6b\Leftrightarrow\left(a-b\right)\left(a+b-2\right)=0\)
\(\Leftrightarrow b=2-a\)
Độ dài đoạn AB là :
\(AB=\sqrt{\left(a-b\right)^2+\left[a^3-b^3-3\left(a^2-b^2\right)\right]^2}\)
\(=\sqrt{\left(a-b\right)^2+\left(a-b\right)^2.\left[a^2+ab+b^2-3\left(a+b\right)\right]^2}\)
\(=\sqrt{4\left(a-1\right)^2+4\left(a-1\right)^2\left[\left(a-1\right)^2-3\right]^2}\)
Đăth \(\left(a-1\right)^2=t\) mà \(AB=4\sqrt{2}\Leftrightarrow t+t\left(1-3\right)^2=8\Leftrightarrow\left(t-4\right)\left(t^2-2t+2\right)=0\)
\(\Leftrightarrow t=4\Rightarrow\left[\begin{array}{nghiempt}a-1=2\\a-1=-2\end{array}\right.\)
\(\Rightarrow\left[\begin{array}{nghiempt}a=3\\a=-1\end{array}\right.\)
* Với \(a=3\Rightarrow b=-1\Rightarrow A\left(3;2\right);B\left(-1;-2\right)\)
* Với \(a=1\Rightarrow b=3\Rightarrow A\left(-1;-2\right);B\left(3;2\right)\)
Vậy \(A\left(-1;-2\right);B\left(3;2\right)\) hoặc \(A\left(3;2\right);B\left(-1;-2\right)\)
 ]
]