Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

U1 = 2.1 - 1 = 1
U2 = 2.2 - 1 = 3
U3 = 2.3 - 1 = 5
U4 = 2.4 - 1 = 7
U5 = 2.5 - 1 = 9

số có dạng \(\overline{abcdef}\left(0\le a,b,c,d,e,f\le9,a\ne0\right)\)
f có 5 cách chọn
TH1 : số lẻ đứng đầu
a có 4 cách chọn
Chọn 2 số lẻ và xếp vào giữa a, f : \(A^2_3\)
Các số lẻ chia ra 3 khoang giữa a và f, cần chọn ra 2 số chẵn xếp vào 3 khoang đó => số cách chọn : \(C^2_5\cdot C^2_3\cdot2!\)
TH2 : số chẵn đứng đầu
a có 4 cách chọn
Chọn 3 số lẻ xếp giữa a và f : \(A^3_4\)
Chọn 1 số chẵn xếp vào 1 trong 3 khoang giữa 4 số lẻ : \(4\cdot3\)
Số các cần tìm : \(5\cdot\left(4\cdot A^2_3\cdot C^2_5\cdot C^2_3\cdot2!+4\cdot A^3_4\cdot4\cdot3\right)=12960\)

a. Không gian mẫu gồm 36 kết quả đồng khả năng xuất hiện, được mô tả như sau:
Ta có: Ω = {(i, j) | 1 ≤ i , j ≤ 6}, trong đó i, j lần lượt là số chấm xuất hiện trong lần gieo thứ nhất và thứ hai, n(Ω) = 36.
b. A = {(4, 6), (5, 5), (5, 6), (6, 4), (6, 5), (6, 6)} ⇒ n(A) = 6
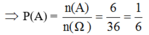
B = {(1, 5), (2, 5), (3, 5), (4, 5), (5, 1), (5, 2), (5, 3), (5, 4), (5, 5), (5, 6), (6, 5)}
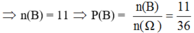
a) Khong gian mau laf (a, b) voi a, b la so cham xuat hien o lan thu nhat va lan thu hai, a, b thuoc {1, 2, 3, 4 ,5 , 6}
b) - Xac suat lan dau xuat hien mat 5 cham la 1/6
- Xac suat de tong so cham cua hai lan gieo bang tong cac xac suat sau: (6,1) + (5,2) + (4,3) + (3,4) + (2,6) + (1,6) = 1/36 + 1/36 + 1/36 + 1/36 + 1/36 + 1/36 = 1/6