Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

b: \(AB=\sqrt{\left(-2-2\right)^2+\left(0-1\right)^2}=\sqrt{17}\)
\(AC=\sqrt{\left(3-2\right)^2+\left(3-1\right)^2}=\sqrt{5}\)
\(BC=\sqrt{\left(3+2\right)^2+\left(3-0\right)^2}=\sqrt{34}\)
\(cosA=\dfrac{AB^2+AC^2-BC^2}{2\cdot AB\cdot AC}=\dfrac{-6}{\sqrt{85}}\)
=>sin A=7/căn 85
\(S_{ABC}=\dfrac{1}{2}\cdot\sqrt{17}\cdot\sqrt{5}\cdot\dfrac{7}{\sqrt{85}}=\dfrac{7}{2}\)
\(AD=\sqrt{\left(4-2\right)^2+\left(5-1\right)^2}=2\sqrt{5}\)
\(DE=\sqrt{\left(-9-4\right)^2+\left(4-5\right)^2}=\sqrt{170}\)
\(AE=\sqrt{\left(-9-2\right)^2+\left(4-1\right)^2}=\sqrt{178}\)
\(cosA=\dfrac{AD^2+AE^2-DE^2}{2\cdot AD\cdot AE}\simeq0,23\)
=>sin A=0,97
\(S_{ADE}=\dfrac{1}{2}\cdot2\sqrt{5}\cdot\sqrt{178}\cdot0,97=29\)
\(OA=\sqrt{2^2+1^2}=\sqrt{5};OB=\sqrt{\left(-2\right)^2}=2\)
AB=căn 17
\(cosA=\dfrac{AO^2+AB^2-OB^2}{2\cdot AO\cdot AB}=\dfrac{9}{\sqrt{85}}\)
=>sin A=2/căn 85
\(S_{OAB}=\dfrac{1}{2}\cdot\sqrt{5}\cdot\sqrt{17}\cdot\dfrac{2}{\sqrt{85}}=1\)
c: vecto AB=(-4;-1)=(4;1)
Tọa độ M là trung điểm của AB là;
x=(2-2)/2=0 và y=(1+0)/2=0,5
Phương trình trung trực của AB là:
4(x-0)+1(y-0,5)=0
=>4x+y-0,5=0
vecto AC=(1;2)
Tọa độ trung điểm của AC là;
x=(2+3)/2=2,5 và y=(1+3)/2=2
Phương trình trung trực của AC là:
1(x-2,5)+2(y-2)=0
=>x+2y-6,5=0
vecto BC=(5;3)
Tọa độ trung điểm của BC là:
x=(-2+3)/2=1/2 và y=(0+3)/2=1,5
Phương trình trung trực của BC là:
5(x-0,5)+3(y-1,5)=0
=>5x+3y-4=0

a/ BĐT sai, với \(c=0\Rightarrow\frac{a}{b}< \frac{a}{b}\) (vô lý)
b/ \(\Leftrightarrow\frac{a^2}{4}+b^2+c^2-ab+ac-2bc\ge0\)
\(\Leftrightarrow\left(\frac{a}{2}-b+c\right)^2\ge0\) (luôn đúng)
c/ Bạn coi lại đề, trong ngoặc bên phải là \(a^2b\) hay \(ab^2\)?
d/ \(a+b+c\ge\sqrt{ab}+\sqrt{bc}+\sqrt{ca}\)
\(\Leftrightarrow2a+2b+2c-2\sqrt{ab}-2\sqrt{bc}-2\sqrt{ca}\ge0\)
\(\Leftrightarrow a-2\sqrt{ab}+b+b-2\sqrt{bc}+c+c-2\sqrt{ca}+a\ge0\)
\(\Leftrightarrow\left(\sqrt{a}-\sqrt{b}\right)^2+\left(\sqrt{b}-\sqrt{c}\right)^2+\left(\sqrt{c}-\sqrt{a}\right)^2\ge0\)
e/ Thiếu điều kiện, BĐT này chỉ đúng khi \(a+b\ge0\) (hoặc a;b không âm)

\(\left\{{}\begin{matrix}a\cdot\left(-1\right)^2+b\cdot\left(-1\right)+c=0\\-\dfrac{b}{2a}=1\\-\dfrac{b^2-4ac}{4a}=-4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a-b+c=0\\b=-2a\\b^2-4ac=16a\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}a-b+c=0\\b=-2a\\4a^2-4ac=16a\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a-b+c=0\\b=-2a\\a-c=4\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}a-b+c=0\\b=-2a\\c=a-4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a+2a+a-4=0\\b=-2a\\c=a-4\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}a=1\\b=-2\\c=-3\end{matrix}\right.\)

Hì hì, thật ra thì mình không biết giúp thằng bạn mình như thế nào nên đành tự đăng câu hỏi vậy :))

a/ Với mọi số thực ta luôn có:
\(\left(a-b\right)^2+\left(b-c\right)^2+\left(c-a\right)^2\ge0\)
\(\Leftrightarrow2a^2+2b^2+2c^2-2ab-2bc-2ca\ge0\)
\(\Leftrightarrow a^2+b^2+c^2\ge ab+bc+ca\)
Lại có do a;b;c là ba cạnh của 1 tam giác nên theo BĐT tam giác ta có:
\(a+b>c\Rightarrow ac+bc>c^2\)
\(a+c>b\Rightarrow ab+bc>b^2\)
\(b+c>a\Rightarrow ab+ac>a^2\)
Cộng vế với vế: \(2\left(ab+bc+ca\right)>a^2+b^2+c^2\)
b/
Do a;b;c là ba cạnh của tam giác nên các nhân tử vế phải đều dương
Ta có:
\(\left(a+b-c\right)\left(b+c-a\right)\le\frac{1}{4}\left(a+b-c+b+c-a\right)^2=b^2\)
Tương tự: \(\left(a+b-c\right)\left(a+c-b\right)\le a^2\)
\(\left(b+c-a\right)\left(a+c-b\right)\le c^2\)
Nhân vế với vế:
\(a^2b^2c^2\ge\left(a+b-c\right)^2\left(b+c-a\right)^2\left(a+c-b\right)^2\)
\(\Leftrightarrow abc\ge\left(a+b-c\right)\left(b+c-a\right)\left(a+c-b\right)\)

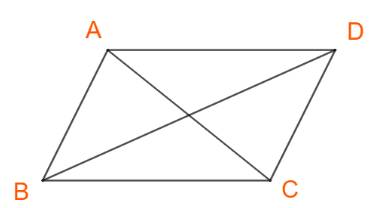
a) Áp dụng định lí cosin ta có:
\(\left\{ \begin{array}{l}A{C^2} = A{B^2} + B{C^2} - 2.AB.BC.\cos ABC\\B{D^2} = A{B^2} + A{D^2} - 2.AB.AD.\cos BAD\end{array} \right.\)
Mà \(AD = BC;\cos BAD = \cos ({180^ \circ } - ABC) = - \cos ABC\)
\(\begin{array}{l} \Rightarrow \left\{ \begin{array}{l}A{C^2} = A{B^2} + B{C^2} + 2.AB.BC.\cos BAD\\B{D^2} = A{B^2} + B{C^2} - 2.AB.AD.\cos BAD\end{array} \right.\end{array}\)
Cộng vế với vế ta được:
\( A{C^2} + B{D^2} = 2\left( {A{B^2} + B{C^2}} \right)\)
b) Theo câu a, ta suy ra: \(A{C^2} = 2\left( {A{B^2} + B{C^2}} \right) - B{D^2}\)
\(\begin{array}{l} \Rightarrow A{C^2} = 2\left( {{4^2} + {5^2}} \right) - {7^2} = 33\\ \Rightarrow AC = \sqrt {33} \end{array}\)


ycbt\(\Leftrightarrow\hept{\begin{cases}9^4a+9^3b+9^2c+9d+e=32078\left(p\right)\\a,b,c,d,e\in N;\le8;a\ne0\end{cases}}\)
VP(p): 9 dư 2 =>e =2
\(\Rightarrow9^3a+9^2b+9c+d=\frac{32078-2}{9}=4564⋮9\Rightarrow d=0\)
\(\Rightarrow9^2a+9b+c=\frac{3564}{9}=396⋮9\Rightarrow c=0\)
\(\Rightarrow9a+b=\frac{396}{9}=44\)chia 9 dư 8 => b=8
=> 9a=36=>a=4
Vậy S =14