Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi số dụng cụ mà 2 xí nghiệp làm theo kế hoạch lần lượt là a ; b ( a ; b > 0 )
Theo bài ra ta có hệ \(\left\{{}\begin{matrix}a+b=720\\\dfrac{12a}{100}+\dfrac{10b}{100}=80\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=400\\b=320\end{matrix}\right.\left(tm\right)\)

Gọi số dụng cụ cần làm của xí nghiệp 1 và xí nghiệp 2 lần lượt là x, y
(x, y ∈ ℕ * x, y < 360, dụng cụ)
Số dụng cụ xí nghiệp 1 và xí nghiệp 2 làm được khi vượt mức lần lượt là 112%x và 110%y (dụng cụ)
Ta có hệ phương trình x + y = 360 112 % x + 110 % y = 400 ⇒ x = 200 y = 160
Vậy xí nghiệp 1 phải làm 200 dụng cụ, xí nghiệp 2 phải làm 160 dụng cụ.
Đáp án: A

Gọi số dụng cụ xí nghiệp I làm theo kế hoạch là x (dụng cụ)
Gọi số dụng cụ xí nghiệp II làm theo kế hoạch là y (dụng cụ)
Điều kiện x;y ∈ N*.
Vì theo kế hoạch hai xí nghiệp phải làm 520 dụng cụ,nên ta có phương trình: x + y = 520 (1)
Thực tế xí nghiệp I vượt mức kế hoạch 10% và xí nghiệp II vượt mức kế hoạch 12%, do đó cả 2 xí nghiệp làm đc 577 sản phẩm nên ta có phương trình:
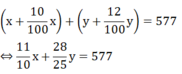
Ta có hệ phương trình
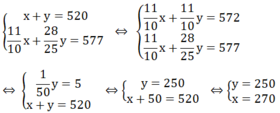
Vậy xí nghiệp I làm theo kế hoạch là 270 dụng cụ.
Xí nghiệp II làm theo kế hoạch là 250 dụng cụ.

Gọi số dụng cụ xí nghiệp 1 phải làm theo kế hoạch là x, số dụng cụ xí nghiệp 2 phải làm theo kế hoạch là y (x, y > 0)
Vì 2 xí nghiệp theo kế hoạch phải làm tổng cộng 360 dụng cụ nên: x + y = 360 (1)
Do số dụng cụ làm được của 2 xí nghiệp trong thực tế vượt mức kế hoạch lần lượt là 10% và 15%:
Suy ra: số dụng cụ xí nghiệp 1 làm được trong thực tế: (100%+10%)x = 110%x
số dụng cụ xí nghiệp 2 làm được trong thực tế: (100%+15%)y = 115%y
Mà tổng số dụng cụ 2 xí nghiệp làm được trong thực tế là 404 dụng cụ
Suy ra: 110%x + 115%y = 404 (2)
Từ (1) và (2) ta có hệ pt:
x+y=360
và 110%x + 115%y = 404
<=> x + y = 360
và 1,1x + 1,15y = 404
<=> x = 200 (thỏa mãn)
và y = 160 (thỏa mãn)
Vậy xí nghiệp 1 phải làm 200 dụng cụ và xí nghiệp 2 phải làm 160 dụng cụ.

Gọi x , y lần lượt là số dụng cụ của xí nghiệp A và B theo kế hoạch .
Trên thực tế :
Xí nghiệp A phải làm \(1,2x\)
Xí nghiệp B phải làm là : 1,1x
Theo bài ra ta có hệ phương trình :
\(\left\{{}\begin{matrix}x+y=720\\1,2x+1,1y=800\end{matrix}\right.\)
Giai hệ ta đc :
\(\left\{{}\begin{matrix}x=80\\y=640\end{matrix}\right.\)
Gọi x , y lần lượt là số dụng cụ của xí nghiệp A và B theo kế hoạch .
Trên thực tế :
Xí nghiệp A phải làm 1,2x1,2x
Xí nghiệp B phải làm là : 1,1x
Theo bài ra ta có hệ phương trình :
{x+y=7201,2x+1,1y=800{x+y=7201,2x+1,1y=800
Giai hệ ta đc :
{x=80y=640

a/ \(P=12\)
b/ \(Q=\frac{\sqrt{x}}{\sqrt{x}-2}\)
c/ Ta có:
\(\frac{P}{Q}=\frac{\frac{x+3}{\sqrt{x}-2}}{\frac{\sqrt{x}}{\sqrt{x}-2}}=\frac{x+3}{\sqrt{x}}\ge\frac{2\sqrt{3x}}{\sqrt{x}}=2\sqrt{3}\)
Dấu = xảy ra khi x = 3 (thỏa tất cả các điều kiện )
a. Thay x = 3 vào biểu thức P ta được :
\(p=\frac{x+3}{\sqrt{x}-2}=\frac{9+3}{\sqrt{9}-2}=12\)
b, \(Q=\frac{\sqrt{x}-1}{\sqrt{x}+2}+\frac{5\sqrt{x}-2}{x-4}\)
\(=\frac{\sqrt{x}-1}{\sqrt{x}+2}+\frac{5\sqrt{x}-2}{\left(\sqrt{x}+2\right)\left(\sqrt{x}-2\right)}\)
\(=\frac{\left(\sqrt{x}-1\right)\left(\sqrt{x}-2\right)+5\sqrt{x}-2}{\left(\sqrt{x}+2\right)\left(\sqrt{x}-2\right)}\)
\(=\frac{x-3\sqrt{x}+2+5\sqrt{x}-2}{\left(\sqrt{x}+2\right)\left(\sqrt{x}-2\right)}\)
\(=\frac{x+2\sqrt{x}}{\left(\sqrt{x}+2\right)\left(\sqrt{x}-2\right)}\)
\(=\frac{\sqrt{x}\left(\sqrt{x}+2\right)}{\left(\sqrt{x}+2\right)\left(\sqrt{x}-2\right)}\)
\(=\frac{\sqrt{x}}{\sqrt{x}-2}\)
c, Ta có :
\(\frac{P}{Q}=\frac{\frac{x+3}{\sqrt{x}-2}}{\frac{\sqrt{x}}{\sqrt{x}-2}}=\frac{x+3}{\sqrt{x}}\ge\frac{2\sqrt{3x}}{\sqrt{x}}=2\sqrt{3}\)
Vậy GTNN \(\frac{P}{Q}=2\sqrt{3}\) khi và chỉ khi \(x=3\)

Câu 1:
a) ĐKXĐ: \(x>0;x\ne9\)
Với x=36 (thỏa mãn ĐKXĐ) thì A có giá trị :
\(A=\dfrac{\sqrt{36}+2}{1+\sqrt{36}}=\dfrac{6+2}{1+6}=\dfrac{8}{7}\)
b) Ta có:
\(B=\left(\dfrac{2\sqrt{x}}{x-\sqrt{x}-6}+\dfrac{\sqrt{x}}{\sqrt{x}-3}\right):\dfrac{\sqrt{x}}{\sqrt{x}-3}=\dfrac{2\sqrt{x}+\sqrt{x}\left(\sqrt{x}+2\right)}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+2\right)}\cdot\dfrac{\sqrt{x}-3}{\sqrt{x}}=\dfrac{x+4\sqrt{x}}{\sqrt{x}\left(\sqrt{x}+2\right)}=\dfrac{\sqrt{x}+4}{\sqrt{x}+2}\)
c) Ta có:
\(P=A\cdot B=\dfrac{\sqrt{x}+2}{\sqrt{x}+1}\cdot\dfrac{\sqrt{x}+4}{\sqrt{x}+2}=\dfrac{\sqrt{x}+4}{\sqrt{x}+1}=1+\dfrac{3}{\sqrt{x}+1}\)
Vì x là số nguyên lớn hơn 0 nên
\(x\ge1\Rightarrow\sqrt{x}\ge1\Rightarrow\sqrt{x}+1\ge2>0\Rightarrow P\le1+\dfrac{3}{2}=\dfrac{5}{2}\)
Dấu bằng xảy ra khi x=1;
Gọi số sản phẩm dự định của xí nghiệp A và B lần lượt là x,y \(\left(x,y\in N;0< x,y< 720\right)\)
Vì tổng sản phẩm dự định là 720 nên ta có phương trình: \(x+y=720\left(1\right)\)
Vì thực tế , xí nghiệp A hoàn thành vượt mức 12% nên số sản phẩm xí nghiệp A thực tế là : \(112\%x=\dfrac{28}{25}x\)
Xí nghiệp B hoàn thành vượt mức 10% nên số sản phẩm xí nghiệp B thực tế là : \(110\%y=\dfrac{11}{10}y\)
Vì tổng số sản phẩm thực tế là 800 nên ta có phương trình: \(\dfrac{28}{25}x+\dfrac{11}{10}y=800\Leftrightarrow56x+55y=40000\left(2\right)\)
Từ (1)(2) ta có hệ phương trình:
\(\left\{{}\begin{matrix}x+y=720\\56x+55y=40000\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x+y=720\\55\cdot720+x=40000\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=400\\y=320\end{matrix}\right.\left(t.m\right)\)
Vậy số sản phẩm 2 xí nghiệp làm theo kế hoạch lần lượt là 400 và 320 sản phẩm