Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

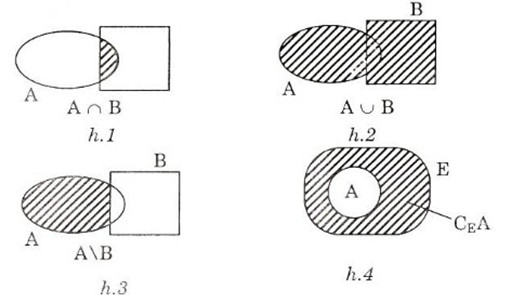
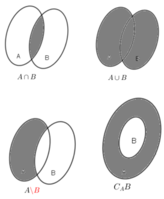
– Giao của hai tập hợp: A ∩ B = {x | x ∈ A và x ∈ B}
– Hợp của hai tập hợp: A ∪ B = {x | x ∈ A hoặc x ∈ B}
– Hiệu của A và B: A \ B = {x | x ∈ A và x ∉ B}
– Phần bù của B trong A: Nếu B ⊂ A thì A \ B gọi là phần bù của B trong A, kí hiệu: CAB.
- Hình minh họa:

Ví dụ về phép thử: Bốc bóng ngẫu nhiên từ trong hộp, bốc bài ngẫu nhiên từ trong bộ bài …..

Có hai cách cho một tập hợp:
+) Liệt kê các phần tử của tập hợp.
Chẳng hạn: A = {0; 1; 2; 3; 4; 5}
+) Chỉ ra tính chất đặc trưng của tập hợp đó.
Chẳng hạn: A = {\(x \in \mathbb{N}|0 \le x \le 5\)}

a) Thay x=100 ta được:
\(y = - {200.100^2} + 92000.100 - 8400000\)
\( = - 1200000\)
Thay x=200 ta được:
\(\begin{array}{l}y = - {200.200^2} + 92000.200 - 8400000\\ = 2000000\end{array}\)
Vậy với \(x = 100\) thì \(y = - 1200000\)
Với \(x = 200\) thì \(y = 2000000\)
b) Với mỗi giá trị của x có 1 giá trị tương ứng của y.

Xét dấu tam thức bậc hai tức là kiểm tra về dấu của tam thức bậc hai theo từng (khoảng) giá trị của ẩn.
Ta có \(a = - 200 < 0,b = 92 000, c = 8400 000\)
\(\Delta ' = {(92000:2)}^2 - \left( { - 200} \right). 8400 000 = 436000000 > 0\)
\( \Rightarrow \)\(f\left( x \right)\) có 2 nghiệm \(x = 230 \pm 10\sqrt 109\). Khi đó:
\(f\left( x \right) < 0\) với mọi x thuộc các khoảng \(\left( { - \infty ; 230 - 10\sqrt 109} \right)\) và \(\left( {230 + 10\sqrt 109; + \infty } \right)\);
\(f\left( x \right) > 0\) với mọi x thuộc các khoảng \(\left( {230-10\sqrt 109; 230 + 10\sqrt 109} \right)\)

Để cửa hàng có lãi thì lợi nhuận lớn hơn 0, suy ra \(I > 0 \Leftrightarrow - 3{x^2} + 200x - 2325 > 0\)
Tam thức \(I = - 3{x^2} + 200x - 2325\) có \(\Delta = 12100 > 0\), có hai nghiệm phân biệt \({x_1} = 15;{x_2} = \frac{{155}}{3}\) và có \(a = - 3 < 0\)
Ta có bảng xét dấu như sau:
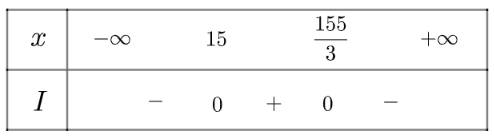
Vậy ta thấy cửa hàng có lợi nhuận khi \(x \in \left( {15;\frac{{155}}{3}} \right)\) (kg)

Các số sinα; cosα; tanα; cotα được gọi là giá trị lượng giác của góc α, với 0o ≤ α ≤ 180o.