Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Cần tác dụng vào nắp một lực thằng được trọng lượng của nắp và lực gây ra bởi sự chênh lệch áp suất giữa không khí bên ngoài và bên trong bình:
F = mg + S( p 1 - p 2 ) = mg + π d 2 /4( p 1 - p 2 ) = 692N

Xét lượng khí trong bình.
Trạng thái đầu: V 1 = 8 lít; T 1 = 100 + 273 = 373 K ; p 1 = 10 5 N/ m 2
Trạng thái cuối: V 2 = 8 lít; T 2 = 20 + 273 = 293 K; p 2 = ?
Vì thể tích không đổi nên:
p 1 / T 1 = p 2 / T 2 ⇒ p 2 = p 1 T 2 / T 1 = 7,86. 10 4 N/ m 2

Đáp án C
Gọi P o và T o lần lượt là áp suất và nhiệt độ ban đầu của khối khí trong bình
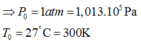
Gọi P và T lần lượt là áp suất và nhiệt độ của khối khí trong bình khi nút bắt đầu bị đẩy lên
![]()
Vì thể tích của khối khí là không thay đổi ngay trước khi nút bị đẩy lên, do đó theo định luật Sác – lơ, ta có:
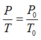

![]()
khi nút bắt đầu bị đẩy lên, ta có:
![]()

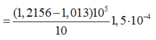
![]()

Đáp án C
Gọi P là áp suất của khối khí ở nhiệt độ
![]()
Vì bình thuỷ tinh được nút kín, nên thể tích của khối lượng trong bình là không thay đổi. Do đó áp dụng định luật Saclo, ta có
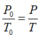
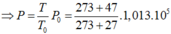
![]()

Xét lượng khí còn lại trong bình
Trạng thái 1: V 1 = V/2; T 1 = 27 + 273 = 300 K; p 1 = 40 atm.
Trạng thái 2: V 2 = V; T 2 = 12 + 273 = 285 K; p 2 = ? atm,
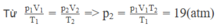

Áp suất ban đầu là \(p_1\left(atm\right)\)
Áp suất lúc sau: \(p_2=\dfrac{1}{2}p_1\left(atm\right)\)
Áp dụng quá trình đẳng tích: \(\dfrac{p_1}{T_1}=\dfrac{p_2}{T_2}\)
\(\Rightarrow\dfrac{p_1}{3+273}=\dfrac{\dfrac{1}{2}p_1}{T_2}\)
\(\Rightarrow\dfrac{1}{3+273}=\dfrac{1}{2}\cdot\dfrac{1}{T_2}\)
\(\Rightarrow T_2=138K\)
Áp suất ban đầu là p1(atm)p1(atm)
Áp suất lúc sau: p2=12p1(atm)p2=12p1(atm)
Áp dụng quá trình đẳng tích: p1T1=p2T2p1T1=p2T2
⇒p13+273=12p1T2⇒p13+273=12p1T2
⇒13+273=12⋅1T2⇒13+273=12⋅1T2
⇒T2=138K
*Trạng thái 1:
T1 = 80 + 273 = 353 K ;
P1 = 105 N/m2.
* Trạng thái 2:
T2 = 20 + 273 = 293 K
P2 = ?
Vì thể tích không đổi, nên theo định luật Sác-lơ, ta có:
\(\frac{P_1}{T_1}=\frac{P_2}{T_2}\)
\(\Rightarrow P_2=\frac{10^5.293}{353}\approx83002\) N/m2
Muốn mở nắp bình cần một lực:
\(F=mg+S\left(P_1-P_2\right)=3.10+\frac{\text{π}.\left(\frac{20}{100}\right)^2}{4}\left(10^5-83200\right)\approx558\left(N\right)\)
#trannguyenbaoquyen